Подаева Наталия Георгиевна
доктор педагогических наук, профессор кафедры алгебры и геометрии, Елецкий государственный университет им. И.А. Бунина, г. Елец podaeva@mail.ru 

Подаев Михаил Валерьевич
кандидат педагогических наук, старший преподаватель кафедры математического анализа и элементарной математики, Елецкий государственный университет им. И.А. Бунина, г. Елец
podaev86@rambler.ru

Социокультурная коммуникация в обучении геометрии младших подростков

Аннотация
Коммуникация рассматривается в двух ракурсах: теоретическом, как феномен, и практическом, как технология социокультурно-ориентированного обучения геометрии младших подростков, имеющая целью создание условий, обеспечивающих сохранение, передачу и воспроизводство геометрических знаний, категорий, методов как социокультурных ценностей. Раскрывается  содержание первого этапа трансляции-коммуникации в рамках курса «Основы геометрии» для учащихся 5-6 классов.

Ключевые слова
ценностное отношение; коммуникация-трансляция ценности; задачи  осознания, обобщения, осмысления.

В настоящее время отечественное математическое образование переживает кризис: все более ощутим разрыв между новыми технологиями, информационными системами и слабой готовностью, мотивированностью основного контингента учителей к новациям, к модификации своего стиля преподавания. В поиске ответа на вопрос, где же ставить запятую в предложении «ломать нельзя модернизировать», консервативно настроенная часть педагогического сообщества призывает к возврату в «старое советское образование» – к сохранению того ценного, что нажито усилиями ученых, учителей и методистов. Вместе с тем разработчики новых образовательных стандартов исходят из необходимости построения образовательной модели опережающего развития, цель которой – поколение с растущими уровнями развития мышления и IQ, формирование эпистемического общества, социализация личности. В плане освоения предметных программ стандарты заменяют саму парадигму школьного образования – речь идет не просто о предметных знаниях, умениях, навыках или компетенциях, речь идет о личностно и социально значимом опыте деятельности. Приятие такой точки зрения позволило нам выработать стратегию обновления содержания школьного математического образования в направлении социокультурной парадигмы и обосновать технологию ее реализации применительно к обучению геометрии младших подростков (см. работы [1], [2]). В русле социокультурной концепции образования, разрабатываемой научной школой В.И. Добренькова, В.И. Нечаева [3], познавательная деятельность представлена как системное образование, компоненты которого одновременно рассматриваются и как фазы цикла культурного освоения субъектом ценностей (носители которых – математические категории, объекты, методы), как динамика деятельности познания – ценностная ориентация, побуждение, коммуникация, адаптация и продуцирование.

Раскроем сущность этапа коммуникации, представляющего звено обратной связи в предложенной динамике освоения ценности. В русле деятельностного подхода коммуникация – это направленная связь субъекта с окружающей действительностью при опредмечивании и распредмечивании информации. В ходе образования происходит овладение социокоммуникативными ситуациями: обучающийся принимает сообщения (фрагмент культурного опыта – дискурс), выполняя функцию реципиента, но для этого учитель должен уметь передавать сообщения («упаковывать» и кодировать их), выполняя функцию коммуникатора. Вместе с тем ученику недостаточно раскодировать сообщение – для его распознавания необходимо обладать внутренним контекстом. Материальными носителями информации выступают определенные предметно-знаковые системы – математическая терминология и символика как языковая форма представления информации, изображение пространственных геометрических фигур в аксонометрии и др. Основная цель коммуникационного процесса – обеспечение понимания информации, поступающей к потребителю, поэтому коммуникация может быть определена как передача не только информации, но ее значения и смысла с помощью символов. Напомним, что значение – это толкование знаков и символов, их сочетаний в математической терминологии. Смысл – это значение, которое знаковые конструкции приобретают для участников коммуникации в различных ситуациях. Значение может долгое время оставаться одним и тем же, а смысл в каждой ситуации оказывается различным. Смысл выражает ценностное содержание сообщения. Смыслы и ценности часто рассматриваются как очень близкие понятия [3, с. 43].

Технология социокультурной коммуникации в ситуации обучения геометрии рассматривается как система функционирования ее компонентов и имеет целью развитие учебной деятельности, позволяющей присваивать способы действия и понимания, необходимые для освоения ценностного содержания геометрических понятий. Центральной основой выступает концепция, в русле которой вектор развития коммуникации можно представить как соединяющий три плоскости (координаты). Первая – «движение» в плоскости социокультурного содержания обучения. Коммуникация рассматривается как фаза цикла,  звено обратной связи в предложенной динамике культурного освоения субъектом ценностей (носители которых – математические категории, объекты, методы). Вторая координата описывает «движение» в психодидактическом контексте. Выделяются уровни обученности (понимания, усвоения и применения материала), представляющие собой целостную систему поэтапного формирования деятельности по освоению математических знаний, умений и культурных способностей. Речь идет о приобретении познавательного опыта, формировании умений как умственных действий, являющихся производными операциями от предметных действий, в связи с чем данные уровни могут быть также описаны и как функции познавательного процесса. Третья координата – движение в плоскости освоения деятельностной компоненты геометрических понятий, их ценностного содержания (смысла).

Концептуальная гипотеза состоит в предположении – эффективность социокоммуникативных процессов в ситуации обучения геометрии, обеспечивающих рефлективное отношение к математическим ценностям – понимание ценностных позиций, – обусловлена целым рядом факторов, среди которых ключевое место отводится реализации психодидактических задач осознания, осмысления и обобщения содержания и процесса деятельности. В качестве базовой выделяется задача осознания – неявное знание: толкование знаков, их сочетаний в знаково-символической системе, отнесение воспринимаемого предмета к соответствующей категории предметов, обеспечение получения учащимся представлений — установление им соответствия между словом и образом, способность образно представлять словесные формулировки, создавать перцепт (образ восприятия); «актуальное осознание» (А.Н. Леонтьев) – способность рефлектировать и осознавать содержание учебного предмета как цель своей деятельности.

Выделим схему организации освоения ценностного содержания геометрических понятий в процессе коммуникации.

1. Мотивация изучения геометрического материала, обеспечивающая механизмы осуществления таких этапов, как ценностная ориентация, побуждение [1]. 

2.  Пространственный компонент коммуникации – уровень представлений. 1) Образ восприятия (перцепт) – представление: «натурализация идеального содержания в знаке» как средство преодоления формализма; создаются условия для понимания обучающимся самой идеальной геометрической модели, фиксированной в чертеже – материализация, представление в виде материального макета, трехмерное компьютерное моделирование. Предполагается освоение учащимися предметных действий с фигурами-вещами, таких как вычерчивание, конструирование, деформация. 2) Обобщенное представление или предпонятие (образ-концепт): преодоление «знаковой натурализации» – так называемая денатурализация; обеспечиваются психодидактические закономерности осознания, осмысления и обобщения содержания и процесса деятельности; формирование топологических представлений об изучаемом геометрическом объекте; осознание учеником символической функции чертежа и освоение способов оперирования с чертежом как со сложным семиотическим объектом (оперирование образом, ориентация в пространстве).

3. Логический компонент коммуникации – вербально-логический уровень. Понятие – система понятий. Формирование геометрических понятий как теоретических: выделение метрических свойств, существенных для осознания изучаемого геометрического объекта; установление связи между топологическими и метрическими свойствами. Выделение понятия, для которого данное является максимальной подсистемой, и понятия, для  которого данное является ближайшим родом. При этом из набора существенных свойств геометрического объекта выделяется достаточный и необходимый набор (желательно не один) и формулируется определение понятия.

В рамках данной статьи рассматривается пространственный компонент коммуникации. Схематично этапы его развития можно представить так: «1) создание перцепта + 2)  оперирование образами + ориентация в пространстве = обобщенное представление или предпонятие – образ-концепт». На первом этапе предполагается освоение учащимися предметных действий с фигурами-вещами, таких как вычерчивание, конструирование, деформация. На втором этапе формируется предпонятие (образ-концепт) – необходимо преодоление знаковой натурализации, что предполагает принципиально другой (по сравнению с предметным действиями) способ восприятия изображений геометрических фигур – операциональный, суть которого в мысленном воссоздании характеристик представленного геометрического объекта, фиксированных в изображении как в знаке-символе (Г.П. Щедровицкий [4]). Для обеспечения операционального способа восприятия целесообразно использование образовательных технологий смешанного типа, интегрирующих традиционное обучение и новые программные средства трехмерного моделирования – статические и динамические интерпретации с использованием технологий мультимедиа. Коммуникация-трансляция информации происходит одновременно на двух кодах – словесном и образном, что обеспечивает включение деятельности правополушарных механизмов – «пиршество образной мысли». При этом обеспечение мысленного воссоздания характеристик представленного геометрического объекта происходит через последовательность развития представлений «от топологических к метрическим через проективные». Напомним, что И.Я. Каплунович исходит из положений Ж. Пиаже об имманентном формировании структур мышления, в соответствии с которыми обучение должно быть согласовано с последовательностью естественно развивающихся структур, то есть начинаться с опоры на топологические структуры, далее – проективные, а уже потом метрические и наиболее сложные – алгебраические [5].

Остановимся подробнее на содержании первых этапов – «создание перцепта (пространственное представление)» и «оперирование образами» – в рамках курса «Основы геометрии» для учащихся 5-6 классов. Предполагается создание образов трехмерных тел, их свойств и отношений путем вос­приятия реальных объектов, их графи­ческих изображений. Реализуется закономерность осознания, предполагающая преодоление формализма, подачу информации одновременно на  двух кодах – вербальном и образном, так называемую «натурализацию идеального содержания в знаке». При этом простран­ственные представления — «прерогатива скорее процессов восприятия и памяти, нежели мышления» (И.Я. Каплунович [5]). Пространственное представление в психологии связывают с воображением – психическим процессом, заключающимся в создании новых образов (представлений) путем обработки материала восприятий и представлений, полученных в предшествующем опыте. Отмечая связь создания перцепта как чувственного образа с фантазией, творчеством, в его структуре выделим смысловые образования (фреймы) – накопленные и упорядоченные прошлые обращения, модели, «осколки» прежних сообщений, чувственные образы, ощущения, представления, эмоции. В качестве основных способов создания образа будем рассматривать: агглютинацию – «склеивание» различных, несоединимых в повседневной жизни частей; гиперболизацию – парадоксальное  увеличение или уменьшение предмета или отдельных его частей; схематизацию – отдельные представления сливаются, различия сглаживаются; типизацию – выделение существенного, повторяющегося  в однородных фактах и воплощение их в конкретных фактах; акцентирование – особое выделение, подчеркивание какой-либо детали, части.  

В ходе опытно-экспериментальной работы были выделены уровни в структуре пространственного компонента коммуникации, определены критерии: полнота – включает в себя количество выделенных объектов, составляющих чувственный опыт младших подростков в восприятии; это выразительные детали, единые связи между признаками; эмоциональность – интенсивность чувств, характеризующих личность, отношение  обучающего к геометрическим объектам, которые проявляются в эмоционально–ценностных суждениях ученика; ассоциативность – наличие близких и далеких ассоциаций, которые возникают у учащихся; оригинальность – новизна, яркость, самобытность, емкость образа, проявляющаяся в своеобразном отборе фактов; гибкость – число переключений с одного класса объектов на другой в ходе ответов. 

На первом уровне (низком) представления развиты недостаточно, образы статичны, ассоциативность осуществляется по названию, по внешним признакам, гибкость и оригинальность мышления не проявляются. Пример задания для диагностики развития представлений на данном уровне: «Вокруг небольшого курортного городка расположены три круглых не соединяющихся между собой озера: большое, средних размеров и маленькое. Отдыхающие, в каком бы направлении ни отправлялись на загородную прогулку, двигаясь по прямой линии, обязательно приходили к одному из озер. Может ли такое быть? Как расположены городок и озера?»

На втором уровне (среднем) развитие представлений характеризуется фрагментарностью, эмоциональное, оригинальное выделяется не всегда, присутствуют выразительные детали. Пример: «Перечертите рис. 1 в тетрадь. Дорисуйте:

а) до 4-х-угольной пирамиды (а);

б) до 5-угольной пирамиды (б);

в) до 6-угольной пирамиды так, чтобы боковые ребра были изображены более наглядно (не накладывались друг на друга) (в);

г) до 4-х-угольной пирамиды, в основании которой – параллелограмм (г)».

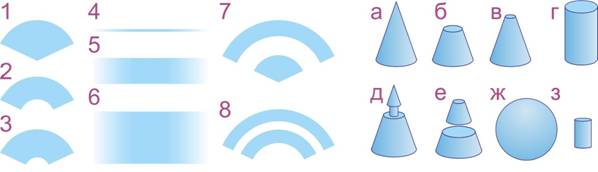
Рис. 1. Изображение пирамиды

На третьем уровне (достаточном) образы яркие, эмоциональные, метафоричные. Проявляется быстрота, гибкость мышления. Происходит оживление предметов. Пример: «На рис. 2 слева изображены следы от различных валиков. Из рис. справа подберите к каждому валик нужной формы».

 

Рис. 2. Сопоставьте форму валика и его след

Рис. 3. Развертка куба

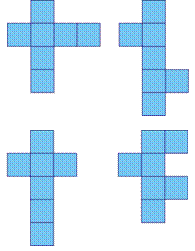
На четвертом уровне (высоком) проявляется оригинальность образов в их разнообразии, метафоричность, появляются абстракции, ассоциативность связывается с прикладным содержанием объектов. Пример: «Посмотрите на фигуры на рис. 3. Мастеру поступили заготовки для коробок кубической формы в виде их разверток. 1) Какие стороны являются лишними? 2) Если нижней гранью коробки является сторона под номером 2, какая сторона окажется наверху?»

Литература

1. Подаева Н.Г. Социокультурная концепция математического образования [Текст] / Н.Г. Подаева. – Елец: ЕГУ им. И.А. Бунина, 2012.

2. Подаева Н.Г., Подаев М.В. Социокультурное содержание школьного математического образования: мыследеятельностные технологии // Письма в Эмиссия. Оффлайн (The Emissia. Offline Letters): электронный научный журнал. 2013. №1(январь). ART 1948.- URL: http://www.emissia.org/offline/2013/1948.htm  - [дата обращения 08.04.2013].

3. Добреньков, В.И. Общество и образование [Текст] // В.И. Добреньков, В.Я. Нечаев. М.: ИНФРА-М, 2003.

4. Щедровицкий Г.П. Опыт логического анализа рассуждений («Аристарх Самосский») [Текст] / Г.П. Щедровицкий //Философия. Наука. Методология. - М.: Шк.Культ.Полит., 1997. — 656 с.

5. Каплунович, И.Я. Психологические закономерности развития пространственного мышления [Текст] / И.Я. Каплунович // Вопросы психологии, 1999, №1.

Исследование выполнено при финансовой поддержке Российского Гуманитарного Научного Фонда, проект № 14-16-48007«Обновление содержания школьного математического образования: социокультурный подход»

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

_____

Natalia G. Podaeva
Doctor of Pedagogical Sciences, Professor of Department of Algebra and Geometry, I.A. Bunin Elets State University, Elets-city 
podaeva@mail.ru   

Michael V. Podaev
Candidate of Pedagogical Sciences, Senior lecturer of Department of Mathematical Analysis and Elementary Mathematics, I.A. Bunin Elets State University, Elets-city 
podaev86@rambler.ru

Socio-cultural communication in teaching geometry younger teenagers

Communication is considered from two perspectives: theoretical, as a phenomenon, and practical, as technology-based socio-cultural learning geometry younger teenagers, aimed at creating conditions for the conservation, transmission and reproduction of geometric knowledge, categories, methods such as social and cultural values. The content of the first stage of a broadcast communication in the framework of the course "Fundamentals of Geometry" for students 5-6 years of schooling.

Keywords: value attitude, communication broadcasting values; task awareness, synthesis, reflection.

Literatura

1.    Podaeva N.G. Sociokul'turnaja koncepcija matematicheskogo obrazovanija [Tekst] / N.G. Podaeva. – Elec: EGU im. I.A. Bunina, 2012.

2.    Podaeva N.G., Podaev M.V. Sociokul'turnoe soderzhanie shkol'nogo matematiche-skogo obrazovanija: mysledejatel'nostnye tehnologii // Pis'ma v Jemissija. Of-flajn (The Emissia. Offline Letters): jelektronnyj nauchnyj zhurnal. - Janvar' 2013, ART 1948 . - CPb., 2013g. - URL: http://www.emissia.org/offline/2013/1948.htm  . – Gos.reg. 0420120031.  - ISSN 1997-8588. - [data obrashhenija 08.04.2013].

3.    Dobren'kov, V.I. Obshhestvo i obrazovanie [Tekst] // V.I. Dobren'kov, V.Ja. Nechaev. M.: INFRA-M, 2003.

4.    Shhedrovickij G.P. Opyt logicheskogo analiza rassuzhdenij («Aristarh Samos-skij») [Tekst] / G.P. Shhedrovickij //Filosofija. Nauka. Metodologija. - M.: Shk.Kul't.Polit., 1997. — 656 s.

5.    Kaplunovich, I.Ja. Psihologicheskie zakonomernosti razvitija prostranstvennogo myshlenija [Tekst] / I.Ja. Kaplunovich // Voprosy psihologii, 1999, №1.