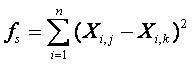Электронный научно-педагогический журнал. Издается с 7 ноября 1995 года.

Электронное научное издание. Зарегистрировано в Федеральном депозитарии электронных изданий ФГУП НТЦ "Информрегистр" Министерства связи и информатизации РФ.
Государственная регистрация  # 0420700031 от 27.11.2006

Механцев Борис Евгеньевич
соискатель по кафедре общей педагогики Таганрогского государственного педагогического института, г. Таганрог

bob_meh@pisem.net  

Формализация создания микрогрупп по результатам тестирования

В рамках настоящей работы  излагается технология формирования учебных групп, основанная на методе приложения кластерного анализа к бинарным массивам, формирующимся в результате тестирования учащихся.  Описываемая технология может применяться  для решения задачи формирования групп, часто возникающей в ходе обучения.

Актуальность исследования обусловлена тем, что с одной стороны, обучение в микрогруппах часто бывает педагогически оправдано и в ряде случаев - даже необходимо, а с другой стороны – разбивка группы учащихся на микрогруппы, как показывает практика, далеко не всегда оптимальна с точки зрения достижения целей группового обучения. Следует подчеркнуть, что, как правило, понимание неоптимальности формирования микрогрупп возрастает по мере продвижения учебного процесса к завершению. Разумеется, опытный преподаватель, хорошо знающий учащихся, сможет провести  разбивку на микрогруппы на основании своего опыта, однако зачастую разбивку необходимо провести в самом начале учебного процесса. Таким образом, налицо противоречие, для разрешения которого необходима разработка процедуры формирования микрогрупп, инвариантной по отношению к опыту преподавателя. 

Целью работы является формализация процесса разбивки учащихся на микрогруппы для  различных учебных целей с использованием технологии, являющейся составной частью процедуры кластерного анализа, исходными данными для которой являются результаты тестирования.

Кластерный анализ в математической статистике— это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое из которых описывается набором исходных переменных Х1,Х2, ..., Хm. Целью кластерного анализа является образование групп схожих между собой объектов, которые принято называть кластерами. Слово кластер английского происхождения (cluster), переводится как сгусток, пучок, группа. Родственные к этому слову термины, используемые в литературе, — класс, таксон, сгущение [1].

Простейший вид кластерного анализа - разбиение учебной группы (например, школьного класса) на отличников, хорошистов и так далее. Очевидно, однако, что примитивность критерия, лежащего в основе такого разбиения приводит к тому, что многие неочевидные, но существенные детали остаются неустановленными.

Дидактические тесты, сопровождаемые бинарным оцениванием ответов (правильно/неправильно, 1/0) в основном решают задачу определения итоговой оценки по результатам тестирования [2]. Тем не менее, большой объем ответов на тестовые задания позволяет использовать результаты тестов с применением технологию кластерного анализа для деления тестируемых на группы с целью:

• интенсивного дообучения по предмету,

• дальнейшего обучения в группах например по технологиям проектного обучения.

Решение обозначенных задач требует подбора в микрогруппы людей по совершенно различным (даже противоположным) критериям.

Действительно, интенсивное дообучение (например, репетиторство) оптимально при одинаковой структуре знаний у совместно занимающихся учеников. Строго говоря, речь идет об одинаковых пробелах в системе знаний, но одинаковые пробелы явно подразумевают и одинаковую структуру имеющихся  знаний.

Проектное же обучение, основанное на работе микрогрупп, совместно решающих сложные задачи, наоборот, будет работать лучше при исходно различающихся структурах знаний у обучаемых. Задача оптимального распределения учеников на микрогруппы для проектного обучения на практике решается по принципу произвольного распределения  - естественного в условиях отсутствии информации. Впрочем, во времена распространенного использования технологии «бригадного обучения» [3] эксплуатировался тезис: «один отличник обеспечивает деятельность всей группы».

Рассмотрим «идеальный конечный результат» для группирования:

• работать должны все участники микрогруппы,

• должен существовать обмен информацией,

• на первом этапе каждый делает то, что у него получается лучше,

• каждый может научить любого другого в микрогруппе.

Для выполнения этих требований необходимо наличие в микрогруппе учеников с максимально различной структурой знаний. Установление структуры знаний до начала серии проектов возможно либо за счет высокой квалификации преподавателя совместно с хорошим знанием учебной группы (включая личные особенности учеников), либо за счет предварительно проведенного исследования уровня и структуры знаний.

Такое исследование может проводиться различными методами, однако в обычной для начала обучения ситуации цейтнота логичным выглядит применение теста, который в данном случае будет являться входным по терминологии Е.А. Михайлычева. Принципиально новым является этап обработки результатов теста с использованием одной из технологий кластерного анализа.

Кластерный анализ в классическом виде устанавливает расстояние между векторами, являющимися представлениями наборов данных и анализирует получившийся набор расстояний. Примеры векторов, определяющих  промежуточные результаты тестирования приведены на рис.1.

Рис. 1. Возможные ориентации векторов при ответах на одно, два и три тестовых задания.  

В нашем случае каждой координатной оси соответствует результат ответа на одно задание. Если ученик ответил на него корректно, по этой оси откладывается «1», если некорректно- «0». Таким образом, вектор является графической интерпретацией записи результатов тестирования в  известной форме

Ученик          Результаты по заданиям
Иванов          1001001111011010101001
Петров          1010101010101010010100
Сидоров       0100011111011010110110

При этом длина вектора равна , где m- число тестовых заданий, на которые дан правильный ответ (см. рис. 1). Единственная постоянно решаемая задача тестирования - подобрать некоторую f(m), то есть функцию оценки от числа правильно решенных тестовых заданий или в данной системе определений - длины результирующего вектора.  Направление вектора оценок определяет структуру знаний и структуру пробелов в таковых.

Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности, то есть минимизации или максимализации расстояния между векторами, определяющими объекты, относящиеся к одному кластеру. Этот критерий может представлять собой некоторый функционал, выражающий уровни приемлемости различных разбиений и группировок, который называют целевой функцией [1]. Как правило, в качестве целевой функции используется внутригрупповая сумма квадратов отклонения, в нашем случае-

где:
Х- результат ответа на i-е тестовое задание j – м тестрируемым,
 - мера расхождения участников,
j и k- номера участников тестирования.

В качестве целевой функции меры расхождения также можно взять безразмерный коэффициент корреляции между массивами результатов ответов на тестовые задания: так определенная целевая функция, с одной стороны, имеет понятный педагогический смысл и, с другой стороны - может быть получена с помощью стандартных процедур для электронных таблиц.

В классической технологии кластерного анализа важным вопросом является проблема выбора необходимого числа кластеров. В нашем случае оно совпадает с числом микрогрупп и  определяется конкретной учебной ситуацией.

Пример анализа.

Имеется результат тестирования пятнадцати студентов. Необходимо разделить их на микрогруппы.

Таблица 1. Матрица результатов:

0 1 0 0 1 0 1 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 1 0 0 1 0 0 1 1 0 1 0 0 0 0 0 1 1

1 1 0 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 1 1 0 1 1 1

0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 1 0 0

0 1 1 1 0 1 0 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1

0 0 1 1 0 0 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 0 1 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1

0 1 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1

1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1

0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 0 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 0 1

0 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0

1 1 1 1 0 1 0 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 1

1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1

0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 0 1 1 0 1 0 1 1 0 1

0 1 0 1 0 0 1 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 1 0

0 0 0 0 0 1 0 1 1 1 0 1 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1

Таблица 2. Матрица корреляции 

Коэффициент корреляции для той или иной пары учащихся  может принимать значения от -1 до 1. Значению «1» соответствует абсолютное совпадение результатов, значению «-1»- абсолютное несовпадение таковых.

Максимальный коэффициент корреляции в данной группе составляет значение 0,7.

Для разбиения всех учащихся на группы для целей доучивания, коэффициент корреляции  внутри группы должен быть как можно выше. Очевидно, что чем выше требование к корреляции результатов учащихся, объединенных в группу, тем больше групп нам придется организовать для доучивания.  В нашем примере, при желании организовать группы с коэффициентом корреляции не ниже 0,3 нам придется организовать четыре группы: А,B,C,D. Результат разбиения будет выглядеть следующим образом:

Номер тестируемого                          1  2  3   4   5  6  7  8   9 10  11 12 13 14 15
Группа, к которой он относится     А  B  B  C  C  D  C  B  D  A    C   C    B  C   B

Микрогруппа «А» получилась небольшой (два человека) из-за того, что ответы ученика №1 схожи с ответами только одного другого ученика (№11) по критерию К>0.3

Приняв за желаемый коэффициент для группирования под проектное обучение отрицательный (или близкий к нулю) коэффициент корреляции (с целью объединения учеников с максимальными различиями в структуре знаний), сформируем из тех же данных микрогруппы

Номер тестируемого                            1  2   3   4  5  6  7  8  9 10 11 12 13 14 15
Группа, к которой он относится       A  B  C  D  C  D  D  A  D  C  A   B   A   C   C

В данном случае, при небольшом числе участников, разбивку можно было провести и вручную, алгоритм же аналогичной операции для машинной обработки должен быть ориентирован на критерий максимального (или соответственно минимального) значения сумм корреляции или другой меры при наперед заданном максимальном размере группы.

Таким образом,  в  данной работе сформулированы простые математические критерии и основанный на них способ разбиения группы учащихся на микрогруппы для различных целей (например, для интенсивного дообучения или для проектного обучения). Способ достаточно прост и может применяться при том условии, что преподавателю известны полномасштабные результаты теста, а не только итоговые оценки. Основным достоинством данного способа является возможность его применения на любом этапе учебного процесса, включая первые установочные занятия.

Литература:
1. Сидоренко Е.В. Методы математической обработки в психологии.// С-Пб, Речь, 2004- 350с.
2. Методология педагогического исследования. // М. Изд-во МП РСФСР, 1986- 310с.
3. Григоренко А.П. В подполье можно встретить только крыс // NY, Детинец, 1967- 280с.

Рекомендовано к публикации:

Г.Ф.Гребенщиков, доктор педагогических наук, научный руководитель работы
А.А.Ахаян, доктор педагогических наук, член Редакционного совета