Гессе Лариса Семёновна
старший преподаватель кафедры гуманитарных, естественнонаучных и математических дисциплин, филиал Московского психолого-социального института в г. Брянске, соискатель по кафедре педагогической психологии,  Московский психолого-социальный институт,
г. Москва
GESSE2007@yandex.ru

Структура и содержание адаптационно-математической компетентности субъекта учебной математической деятельности

Аннотация
Рассматривается вопрос о структуре и содержании адаптационно-математической компетентности субъекта учебной математической деятельности. Представлена взаимосвязь модельного и компетентностного подходов  в процессе формирования математической деятельности учащихся. В процессе формирования компетентности выявлена схема исследования моделей-уравнений. Исследована одна из методических закономерностей формирования компетентности в математике.

Ключевые слова
учебная математическая деятельность, адаптационно-математическая компетентность, структура компетентности, математическая модель

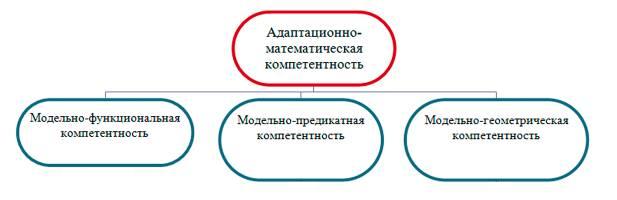
В системе основных направлений модернизации Федеральный компонент государственного стандарта общего образования определяет «формирование ключевых компетенций – готовность учащихся использовать усвоенные знания, умения и способы деятельности  в реальной жизни для решения практических задач» [1. С. 5]. В предметном содержании общего образования компетентностный подход нормативно закреплён и определяет содержание обучения учащихся в виде системы компетентностей, однако и в содержательном, и в технологическом планах его разработанность весьма неполна.

В поисках путей исследования компетентностей и компетенций многие учёные различают их структуру (наличие каких составляющих предполагает данная компетентность или компетенция) и способ её проявления [2. С. 31, С.33]. В связи с этим, при построении структуры и содержания компетенций учебной математической деятельности нами выделены как структурные компоненты (составляющие) исследуемой компетентности, так и способы её проявления: в виде компетенций, что в дальнейшем будет представлено в виде умений на схеме. Такое построение неслучайно и потому, что компетенция проявляется в умениях. «В модели «компетенция-умение» только умение доступно наблюдению, фиксации и оценке» [3. С. 60].

Адаптация  предполагает процесс вхождения человека в определенную среду и его взаимодействие с ней. Человек активно относится к окружающей среде, преобразует ее, только при этом условии возможно взаимодействие человека со средой. Адаптационно-математическая компетентность предполагает способность субъекта математической деятельности применить математику в практической деятельности и для продолжения образования, а для этого необходимо использовать математику как инструмент познания.

Как известно, математика изучает модели, т. е. мысленные конструкции реального мира. Эти модели адекватны отражаемому ими объекту в определённом смысле: «этот смысл определяется существенными качествами объекта, положенными в основу построения модели» [4. С. 7]. При этом математика предлагает набор моделей, т. е. представляет собой мощный аппарат, позволяющий практически любой области знания утверждать старые положения или обнаруживать ранее не познанные закономерности. И если рассматривать математику как инструмент познания, предлагающую модели, из которых каждая отражает те или иные стороны действительности, то в школьном курсе математики изучается модель – функция, модель – предикат (уравнение, неравенство, система уравнений), модель – геометрическая фигура. Следовательно, в структуре адаптационно-математической компетентности, можно выделить составляющие: модельно-функциональную компетентность; модельно-предикатную компетентность; модельно-геометрическую компетентность (Рис. 1).

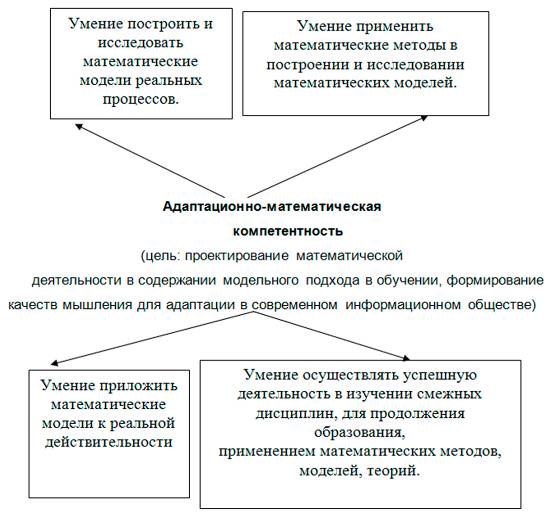
Рис. 1. Структурные элементы адаптационно-математической компетентности.

От структурных компонентов (составляющих) исследуемой компетентности необходимо перейти к способам её проявления. Для этого рассматривая математику как инструмент познания, исследуем механизм работы этого инструмента.

В процессе применения математики к конкретной практической задаче А. Г. Мордкович и ряд других авторов выделяют три этапа: формализацию, внутримодельное решение и интерпретацию [5. С.100]. Методическая закономерность формирования модельного подхода, в случае если модель – уравнение или класс уравнений, имеет вид  схемы:

Фиксируется определённый процесс → Строится математическая модель в форме уравнения, класса уравнений → Осуществляется внутримодельное решение → Производится интерпретация результатов в содержании изучаемого процесса.

Данные этапы позволяют выделить способы проявления адаптационно-математической компетентности (Рис. 2).

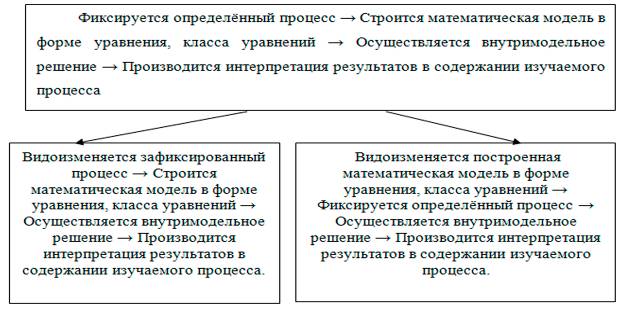
Рис. 2. Способы проявления адаптационно-математической компетентности.

Отметим, что одним из существенных недостатков в школьном курсе математики в России является то, что задачи уже сформированы на языке модели. Таким образом, зачастую отсутствует этап формализации и интерпретации. Многие учёные сходятся в том, что наши учащиеся обладают большим объёмом математических знаний в средней школе, но не умеют выходить за пределы учебных ситуаций, применить знания в действии, т. е. компетентность.

В результате проведения нескольких международных сравнительных исследований образовательных достижений учащихся в области математики удалось выявить, что «в ряде случаев задача была сформулирована таким образом, что учащиеся не могли отнести её к какому-либо разделу математики, чтобы для её решения воспользоваться соответствующими теоретическими фактами, т.е. значительная часть ребят затруднилась составить математическую модель предлагаемой ситуации» [6. С.76]. Таким образом, модельный подход к решению математических задач в том виде, как он представлен в средней школе на сегодняшний день, не вполне соответствует тому требованию, которое предъявляются к математическому образованию в школе сегодня, а именно, «безболезненной адаптации его (ученика) к условиям жизни в современном обществе» [7.  С. 8].

Исследуя компетентность, Джон Равен писал, что «самое главное, что надо подчеркнуть, пытаясь прояснить природу компетентности, это то, что ни один человек не будет действовать именно так, если он глубоко и лично в этом не заинтересован…На практике же содержание деятельности, имеющую личную ценность, может быть достижение конкретного результата… или способа поведения…» [8. С. 67]. Для достижения результата или способа деятельности в математике наиболее ценной представляется для нас организация деятельности ученика по самостоятельному  изменению сюжетной задачи в процессе освоения модельного подхода. Изменение сюжета задачи – это, во-первых, составление новой задачи, т. е. постановка проблемы. Постановка проблемы способствует сдвигу с предметной стороны труда ученика на его психологическую сферу: повышается интерес, проявляются волевые качества и т. д. Деятельность ученика становится наиболее продуктивной, что является условием для развития его мышления и личности в целом. Значение умения ставить проблему отмечается многими учёными. Так, по мнению М Венгеймера, «будущие  системы искусственного интеллекта смогут решать любые проблемы, но они не смогут их ставить. Постановка проблемы - это прерогатива человека [9. С. 24-25]. Изменение сюжета задачи – это, во-вторых, самостоятельное конструирование информации. Важность умения самостоятельно видоизменять информацию подчёркивают и исследователи компетентностного подхода: «Поскольку знания быстро устаревают, а общественные потребности быстро меняются…должны прийти такие методы обучения, сутью которых является…осмысление и анализ учащимися исходной учебной информации, установление путей её видоизменения, приобщение учащихся к самостоятельному конструированию информации в предметной области» [10. С. 57]. И, наконец, в-третьих, задания на изменение сюжета задачи сопряжены с процессом творчества, вследствие этого могут быть сами по себе мотивирующими на выполнения для большинства учащихся.

В проведённом нами эксперименте в процессе формирования математической деятельности по составлению задач, моделью которых является квадратное уравнение, учащиеся 8 класса убедились в том, что после соответствующего преобразования сюжета можно получить модель, взаимосвязанную с ранее построенной или после соответствующего преобразования модели – квадратного уравнения, можно получить задачи с определённым сюжетом. Методическую закономерность  формирования адаптационно- математической компетентности можно представить в виде  схемы (Рис. 3).

Рис. 3. Методическая закономерность формирования адаптационно-математической компетентности (на примере алгебраических уравнений как моделей).

Из приведённой схемы видно, что процесс формирования адаптационно- математической компетентности  учащихся выходит за рамки  модельного подхода в школьном курсе математики (данный процесс шире модельного подхода и включает его в себя).

В заключении отметим, что «…усвоения практических знаний явно недостаточно для приобретения математической компетентности, т. е. эти знания составляют только её часть, а компетентность включает ещё и умения применить свои знания в ситуациях, отличных от тех, в рамках которых они были получены» [6. С. 77]. Формирование адаптационно-математической компетентности призвано помочь нашим ученикам выйти за пределы привычных для них учебных ситуаций и успешно справляться с тестами, включёнными в международные исследования математической грамотности школьников, а также с любыми другими заданиями, предложенными на экзаменах различного уровня.

Литература

1. Сборник нормативных документов. Математика / сост. Э.Д.Днепров, А.Г.Аркадьев.- М.: Дрофа, 2004.- 79с.

2. Спенсер-мл., Лайл М. Компетенции на работе. / Лайл М. Спенсер-мл., Сайн М. Спенсер; пер. с англ. – М.: HIPPO, 2005.- 384c.

3. Государственные образовательные стандарты в системе общего образования. Теория и практика / под ред. В.С.Леднёва, Н.Д.Никандрова, М.В.Рыжакова.- М.: Изд-во Московского психолого-социального института; Воронеж: МОДЕК, 2002.-384с.

4. Фирсов В.В. О прикладной ориентации курса математики / В. В.  Фирсов // Математика в школе.-2006.-№6.- С.2-9.

5. Мордкович А.Г. Профессионально-педагогическая направленность специальной подготовки учителя математики в педагогическом институте: дис…докт. пед. наук: 13.00.02 / Мордкович Александр Григорьевич.- М., 1986.- 355с.

6. Краснянская К.А. Сравнительная оценка математической грамотности 15-летних учащихся в рамках международного исследования /  К.А.Краснянская, Л.О.Денищева  // Математика в школе.-2005.-№3.- С.70-77.

7. Дорофеев Г.В. Профилированная школа в Концепции школьного математического образования / Г.В.Дорофеев, Л.В.Кузнецов, Е.А.Седов // Профильная школа. -  2004. -  №1. – С. 7-14.

8. Равен Дж. Педагогическое тестирование: Проблемы, заблуждения, перспективы / Дж. Равен.- М.: Когито- Центр, 1999.- 144с.

9. Вертгеймер М. Продуктивное мышление / М. Вертгеймер; пер. с англ.; общ. ред. С.Ф.Горбова, В.П.Зинченко; [вступ. ст.  В. П. Зинченко].- М.: Прогресс, 1987.- 336с.: ил. 213.

10. Дьяченко Г.М. Компетентностный подход к формированию логической культуры учащихся в процессе изучения информатике: дис…канд. пед. наук: 13.00.02 / Галина Михайловна Дьяченко.- Омск, 2005.

Рекомендовано к публикации:
А.В.Гоголева, доктор педагогических наук, научный руководитель работы
Н.Ф.Радионова, доктор педагогических наук, член Редакционной Коллегии

-----

Larisa S.Gesse  
senior lecturer of the humanities and natural- mathematical sciences department of the Bryansk branch of Moscow Psychological Social Institute, Moscow
GESSE2007@yandex.ru

The structure and contents of the adaptive-mathematical competence of of the subject of the school mathematics activity

The question on structure and the maintenance of  the adaptive-mathematical competence of the subject of educational mathematical activity is considered. The interrelation modelling and competence  approaches during formation of mathematical activity of pupils is presented. During formation of competence the scheme of research of models-equations is revealed. One of methodical laws of formation of competence of the mathematician is investigated.

Keywords: educational mathematical activity, adaptive-mathematical competence, structure of competence, mathematical model