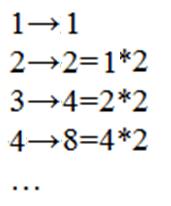Злобина Дарья Александровна
аспирант   кафедры   методики   обучения   математике,   Российский   государственный  педагогический  университет  им.  А.И.  Герцена, С-Петербург
arkadiyas@mail.ru

Задачи на перекодирование как средство, способствующее пониманию учебного материала при изучении алгебры в основной школе.

Аннотация
В статье рассмотрена проблема понимания учащимися математической информации, приведены и обоснованы условия, способствующие пониманию учащимися алгебраического материала, и их реализация посредством задач на перекодирование, приведена классификация этих задач.

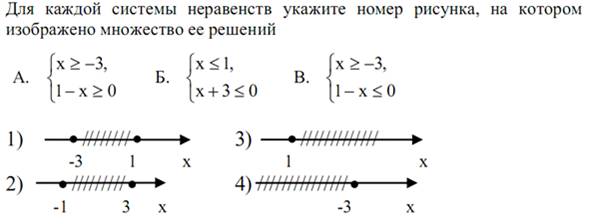
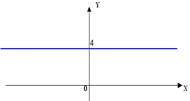
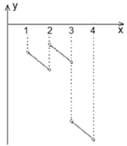
Ключевые слова:
понимание, способы представления информации, задачи на перекодирование, субъектный опыт, перецентровка, децентрация

Обеспечение понимания всегда было одной из основных задач обучения математике. Эта задача конкретизирована в государственных стандартах второго поколения [1], а в диагностических работах по алгебре (едином государственном экзамене и государственной итоговой аттестации (ЕГЭ и ГИА)) появились задания, предполагающие диагностирование понимания учащимися учебного материала через представление задачного материала различными способами.

В качестве примера такой диагностики рассмотрим задание, в котором учащемуся предлагается установить соответствие между символьным и образным заданием системы неравенств (рис. 1)

 

 

Рис.1. ГИА, 2011г. Ответ: А-1), Б-4); В-3).

С каждым годом количество заданий, требующих перевода с одного способа представления информации на другой, растет, но, согласно результатам исследования международной программы по оценке образовательных достижений учащихся (Programme for International Student Assessment, PISA), ЕГЭ и ГИА, не все учащиеся справляются с ними.

Анализ учебников по алгебре показал, что:

1. Текст большинства задач задан одним способом представления информации, либо предполагает перевод между двумя способами представления информации.

2. Задания включают не полный объем понятий (например – в заданиях с выбором функций: отсутствуют точечные функции, почти не встречаются кусочно-непрерывные функции).

3. Почти не встречаются задачи, в которых используются три формы представления информации.

4. Нет методики использования заданий на перекодирование для овладения различными формами представления информации и развития стилевой гибкости.

В исследованиях PISA так же выделены недостатки в умениях российских школьников применять полученные в школе знания в контексте жизненных ситуаций, низкие результаты выполнения заданий, связанных с пониманием информации, представленной различными способами.

Чтобы разработать способы устранения этих недостатков, необходимо обратиться к самому понятию «понимания». Анализ психологической, педагогической и философской литературы показал, что однозначного определения этого термина нет. Многие авторы трактуют понимание как усвоение или как продуктивное усвоение. Некоторые авторы понимание рассматривают как первый этап изучения материала, некоторые как заключительный. Наиболее удачным нам представляется определение этого понятия М.И. Дьяченко и М.А. Кандыбовией: «Понимание – психический процесс включения информации о чем – либо в прежний опыт, в усвоенные ранее знания и постижение на этой основе смысла и значения события, факта, содержания воздействия» [2]. То есть понятие «понимание» опирается на понятия «смысл», значение, связи между ними, а значит требует обращения к логике. Всякое понятие обозначает некоторый объект (называемый значением) и выражает некоторый смысл [3].  Связь между термином, его значением и смыслом обычно изображают в виде семантического треугольника (треугольника Фреге). Но логика обычно рассматривает понятия, связанные с реальными объектами. Математика же изучает объекты, которые реально не существует. Они  - плод ума человеческого. Поэтому в качестве значений математических имен целесообразно рассматривать абстракции, идеи, которые отражены в математических понятиях: понятие числа, понятие треугольника, и т.д. Смысл математических понятий может быть выражен определениями,  признаками, наборами существенных для понятия свойств. Известно, что каждое математическое имя (понятие) характеризуется содержанием и объемом. Объем – множество объектов, выделяемых и обобщаемых в понятии. Содержание – множество свойств, существенных для понятия. [4] Поэтому, фактически, значение имени отражено в объеме понятия, а смысл - в содержании понятия. Однако, ввиду существования многозначности слов (имен понятий) и особенностей восприятия информации, смысл новых понятий, как и новой информации, постигается, согласно психологическим исследованиям (Якиманская И.С.), в первую очередь, в рамках субъектного опыта (СО) учащихся, а потому фактически мы имеем «преобразованный» треугольник Фреге (рис.2).

 

 

 

 

 

 

 

Рис.2. Треугольник Фреге. 

На основании полученной схемы нами была уточнена трактовка понимания алгебраического материала и выделены две составляющие процесса понимания при изучения алгебры:

1. Понимание, как процесс встраивания алгебраических знаний в субъектный опыт (СО) ученика.

2. Понимание, как владение разными значениями алгебраических понятий (отраженными в объеме понятия) и постижение разных смыслов алгебраических понятий и установление связей между ними.

Исходя из уточненного определения понимания, задания на проверку понимания должны позволить ответить на вопросы:

1. Встроился ли новый материал в СО учащегося, то есть стали ли значения понятия частью СО учащегося.

2. Может ли учащийся переходить от одного смысла к другому, постигать разные смыслы и значения и устанавливать связи между ними?

Как же можно обеспечить понимание при изучении алгебраического материала? Каковы условия достижения этого процесса? Способность учащегося переходить от одного от одного смысла к другому определяет умение перекодирования (т.е. умение переходить от одного способа представления информации к другому). Поскольку значение математического понятия – вещь не материальная (абстракция), и, хотя характеризовать понятия принято через содержание и объем, объем алгебраического понятия мы задаем различными способами представления. Фактически это и есть смысл (здесь и далее мы будем рассматривать перекодирование именно в таком, широком смысле). Согласно психологическим исследованиям (М.А. Холодной, И.С. Якиманской), понимание информации определяется индивидуальными особенностями человека. Индивидуальные особенности в познании отражаются в познавательных стилях, которые, являясь индивидуально-своеобразными способами изучения реальности, отвечают за восприятие, переработку и усвоение информации [5]. Персональный познавательный стиль является результатом интеграции разных уровней стилевого поведения, и в его основе его лежат стили кодирования информации, которые отвечают за получение информации извне. Поэтому умение перекодировать информацию является базовым средством обеспечения понимания информации.

Мы выделяем четыре условия, выполнение которых будет способствовать достижению понимания алгебраического материала. 

Первым условием обеспечения понимания является представление текста задач разными способами (формами) кодирования. Любая информация может быть представлена в том или ином виде, который определяется способом ее кодирования [6]. Алгебраическая информация может быть представлена

• словами,

• с использованием математических символов,

• с помощью рисунков, графиков.

Способы кодирования математических текстов называют соответственно: словесным, символьным и образным. Причем в образном способе можно выделить два подвида с разным уровнем сложности восприятия информации: кодирование  с помощью реалистических рисунков и кодирование  с помощью графиков, схемам, чертежей, диаграмм, таблиц. Последний способ предполагает сформированность у учащихся умения читать «легенду», заданную явно или неявно. Такой способ кодирования называется образно-графическим. Образный способ, не предполагающий умение учащихся читать легенду, называется образно-иконическим. [7]

Под символическим способом кодирования мы имеем в виду способ представления информации, предполагающий запись задачного материала на алгебраическом языке, под словесным – задачи и задания, представленные на естественном языке.

Поскольку мы хотим достичь обеспечения понимания учащимися учебного материала, необходимо, чтобы их знания выстроились в систему. Для этого нужно, чтобы эти знания стали частью СО учащихся. Потому при введении нового материала для понимания его учащимися необходимо учитывать СО школьников, поскольку с каждым значением термина ребенок связывает свой смысл. Связь с СО – второе условие обеспечения понимания. Необходимость его выполнения определяется в первой составляющей уточненной трактовки понимания.

В качестве примера использования СО при введении понятия геометрической прогрессии можно предложить учащимся следующую задачу:

Рассмотрим ситуацию, знакомую большинству из вас - распространение в Интернете писем счастья: на первом этапе один человек отправляет письмо с требованием переслать письмо двум другим людям, на втором каждый из них получает письмо, чтобы послать это письмо двум своим знакомым, на третьем уже четыре человека – двум своим и т.д.

                                                                                                    

 

 

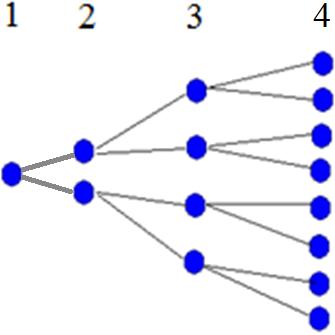
Рис. 3. Представление материала задачи в образно-иконической форме.

                                                               

 

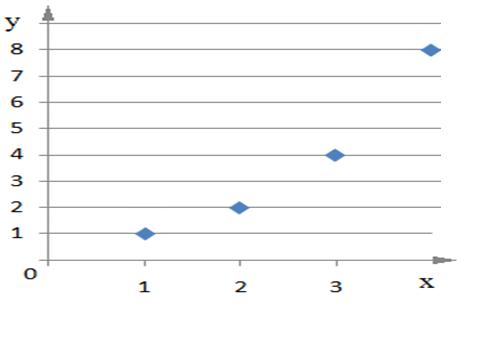
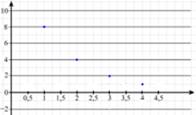
Рис. 4. Представление материала задачи в образно-графической форме

                             

 

Рис. 5. Представление материала задачи в символьной форме.

Данная зависимость изначально представлена в словесной форме, которая, скорее всего, наиболее близка опыту учащихся. Первое изображение словесного процесса представлено в образно-иконической форме (рис.3), второе – в образно-графической (рис. 4). Далее следует символьная запись (рис. 5). Таким образом, в данном примере приведена сначала словесно-образная, потом – внутриобразная (из образно-иконической в образно-графическую), а в конце – образно-символьная перекодировки одного и того же процесса. Если при введении нового материала давать учащимся параллельно все способы представления, то среди них окажется и тот,  способ представления информации, который будет наиболее близок к их СО, что позволит учащемуся в дальнейшем, опираясь на этот способ, усваивать и другие способы представления изучаемого материала.

 

Одно и то же понятие (имя) может иметь разные смыслы, поэтому процесс понимания предполагает как постижение смыслов, так и умение переходить от одного смысла к другому, от одного способа представления к другому. Поэтому следующее условие обеспечения понимания – включение в учебный процесс перецентровки, «перемещения мысленного центра ситуации от одного элемента к другому». [8] Согласно А.А. Брудному, перецентровка является одним из механизмов понимания информации. При перецентровке структура отражаемой в тексте ситуации предстает в изменяющемся виде, т.е. происходит изменение изначальной структуры текста, смещение центра с одного акцента на другой. Она дает возможность взглянуть на тему под другим углом, увидеть новые связи между теми же понятиями, а значит и новые смыслы. Это условие целесообразно реализовывать на этапе повторения учебного материала. При изучении любой темы всегда задается определенное основание для подачи ее как системы. Например, тема «Функции» в 7-9 классах структурируется через такое основание как аналитическое задание функции (вид функции):
1. Линейная функция;
2. Квадратичная функция;
3. Степенная функция;
4. Прогрессия (рассматривается как функция на отрезке натурального ряда, или на всем ряду).

Систематизацию темы целесообразно организовать, выбрав другое основание, например – свойства функций:
1. Область определения функции;
2. Множество значений функции;
3. Нули функции;
4. Монотонность;
5. Промежутки знакопостоянства;
6. Непрерывность;
7. Четность/нечетность.

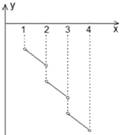
Организуя обобщение темы, опираясь на это основание, учащиеся будут овладевать новыми смыслами. Приведем пример задания на установление связей между свойствами функций:

Установить соответствие между заданными функциями (1-6) и промежутками их убывания (а-е)

 

1	2	3
	, где хÎ[1;4]
4	5	6

1. Числа натурального ряда, меньше пяти.

2. R

3. Пустое множество.

4. (1;2)È(2;3)È(3;4)

5. Множество х: 1≤х≤4

6. Другое.

Эта задача на установление соответствий. В тексте задачи требуется установить связи между информацией, представленной всеми тремя способами кодирования.

Следующим условием, способствующим достижению понимания, является условие необходимости использования задач, реализующих принцип децентрации, предполагающий отсутствие мысленного центра в наборе задач. Как и перецентровка, децентрация предполагает переход от одного смысла к другому и этот принцип целесообразно реализовывать на этапах обобщения и систематизации материала. В отличие от предыдущего, выполнение этого условия направлено на развитие у учащихся умения выделять разные смыслы понятий самостоятельно и устанавливать связи между разными смыслами разных понятий. Для этого учащимся предлагается определить отношения между понятиями, для которых не задано общее основание или не выделено общее свойство. Решение этих задач требует постоянного перехода от одного смысла понятия к другому. Задачи такого типа могут предлагаться, как задания, проверяющие понимание в рамках второй составляющей уточненной трактовки этого понятия. В качестве примеров заданий, реализующих принцип децентрации, можно рассмотреть следующие задачи:

1. Изобразить при помощи кругов Эйлера множества:
   а. Четных функций;
   б. Функций вида  

   в. Квадратичных функций;
   г. Функций, которые являются константами;
   д. Функций вида  

   е. Функций, имеющих не более двух корней.

2. Изобразить при помощи кругов Эйлера множества:
   а. Строго возрастающих функций;
   б. Прогрессий;
   в. Функций;
   г. Точечных функций.

Эти задачи относятся к задачам на перекодировки (словесно-образные и символьно-образные). В них требуется перевести информацию, представленную словами и символами на образно-иконический язык. У учащихся эти задания вызывают наибольшую сложность, поскольку при его решении они должны будут рассматривать заданные множества функций с точки зрения различных смыслов: свойств функций, заданий функций, видов функций, а значит устанавливать связи между разными смыслами разных понятий. Такие задания, с одной стороны, способствуют пониманию, с другой стороны – систематизируют знания и умения учащихся.

Выделенные нами условия образуют в совокупности единую систему требований к задачному материалу на уроках алгебры, но реализуются эти условия через систему задач на перекодирование, поэтому задачи на перекодирование являются важным средством, способствующим пониманию учебного материала при изучении алгебры основной школы. Опишем типологию задач, текст которых представлен различными способами. Все задачи мы разделили на три типа.

К первому типу мы отнесли задачи, информация в которых представлена преимущественно одним способом кодирования (образным, символьным или словесным) и предполагающие решение этим же способом.  Перекодировки как в условии, так и при решении этих задач отсутствуют. Стоит учесть, что задач, представленных исключительно образным способом кодирования, не существует: все задачи, представленные этим способом, предполагают словесные комментарии (например, формулировка задания «достроить график четной функции»). Однако решение этих задач будет представлено исключительно образным способом. 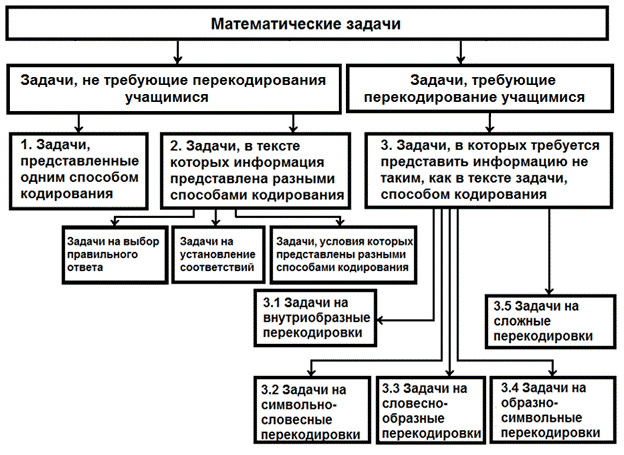Так же мы учитываем, что в задачах, информация в которых представлена словесно, будет присутствовать числа: исторически сложилось, что числа воспринимаются нами так же естественно, как и слова.
Ко второму типу мы относим задачи, в тексте которых информация представлена разными способами кодирования. При решении задач такого типа учащийся не должен перекодировать информацию из одного способа в другой: ему нужно будет лишь сориентироваться в уже представленных определенным способом информации, найти решение задачи. Информация в условии этих задач представлена разными способами кодирования, самостоятельные перекодировки при решении задачи отсутствуют.
К третьему типу мы относим задачи, как следует из заглавия, при решении которых учащийся должен будет перекодировать информацию и представлять ее не таким, как в условии, способом (или способами) кодирования. В свою очередь, в зависимости от того, между какими способами представления происходит перекодировка, задачи третьего типа можно разделить на следующие подтипы: задачи на внутриобразные, символьно-словесные, словесно-образные и сложные перекодировки. К последнему подтипу относятся задачи, при выполнении которых учащиеся должны перекодировать информацию более одного раза.

Таким образом, разработанная нами типология (рис. 6) может быть представлена следующей схемой:

Рис. 6. Типология математических задач.

Литература

1. Стандарты второго поколения. Примерные программы по учебным предметам. Математика. 5-9 классы. М., «Просвещение» 2010. Стр. 4, 8

2. Дьяченко М.И., Кандыбовия Л.А. Психологический словарь-справочник. М.,2001. Стр. 266

3. Переверзев В.Н. Логистика. Справочная книга по логике. М., 1995. Стр. 64

4. Стефанова Н.Л., Подходова Н.С., Орлов В.В. и др. Методика и технология обучения математике. Курс лекций. Москва, «ДРОФА», 2005. Стр. 111

5. Холодная М.А. Когнитивные стили. О природе индивидуального ума. 2-е издание. «Питер», 2004. Стр. 294

6. Холодная М. А. Психология интеллекта. «Питер», 2002. Стр.111

7. Пирс Ч.С. Избранные философские произведения. Москва, «Логос», 2000

8. Брудный А.А. Психологическая герменевтика. М., 1998. Стр. 140

Рекомендовано к публикации:
Н.С.Подходова, доктор педагогических наук,  научный руководитель работы
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

_____

Darya A. Zlobina,
Post-graduate student of Chair of a Technique of Training of Mathematics, Al. Herzen State Pedagogical University of Russia, St.Petersburg
arkadiyas@mail.ru

Transcoding tasks as an aid to understanding the study material for the study of algebra elementary school

The article deals with the problem understanding students ' mathematical information, and are conducive to understanding students ' algebraic material, and their implementation through the tasks in the recoding is the classification of these tasks.

Keywords: understanding, ways of presenting information on the problem encoding, subjective experience, peretsentrovka, decentration