Подаева Наталия Георгиевна,
доктор педагогических наук, профессор кафедры алгебры и геометрии, Елецкий государственный университет им. И.А. Бунина, г.Елец
podaeva@mail.ru  

Подаев Михаил Валерьевич,
кандидат педагогических наук, старший преподаватель кафедры математического анализа и элементарной математики, Елецкий государственный университет им. И.А. Бунина, г.Елец
podaev86@rambler.ru

Социокультурное содержание школьного  математического образования: мыследеятельностные технологии 

Аннотация
Познавательная деятельность в области математики представлена как системное образование, компоненты которого одновременно рассматриваются и как фазы цикла культурного освоения субъектом ценностей: ценностная ориентация, побуждение и др. Раскрывается содержание первого этапа – ценностной ориентации – на примере мыследеятельностной технологии обучения основам геометрии в 5-6 классах.  

Ключевые слова
социокультурное содержание математического образования; освоение универсальных учебных действий;  ценностная ориентация;  мыследеятельностное содержание обучения математике; бихевиористский подход; теория функциональных систем

Как свидетельствуют результаты Международных исследований достижений школьников TIMSS-2011, ученики 4-х классов российских школ занимают десятое место по математике, а восьмиклассники – шестое. Результаты интересны тем, что ставят перед российской системой образования ряд вопросов. Например, надо ли нашей школе избавляться от излишней академичности? Должна ли быть школа гомогенной, когда дети миллионеров и дворников учатся в одном классе? Актуальна ли для России гуманистическая проблема всеобщего образования?  

Известно, что еще Платон считал наиболее важной задачей государства распределение обязанностей в соответствии с врожденными способностями. Современное меритократическое общество близко подошло к осуществлению этой идеи. Российское государство выдвинуло доктрину: от развития одаренной личности – к формированию одаренного общества, от образования элиты – к элитарному образованию. Вопрос в том, не противоречит ли эта доктрина гуманистической идее обеспечения открытого доступа масс к образованию?

Напомним, что в 2012 году направлением тестирования PISA была математика. С каждым годом Россия по результатам PISA оказывается на все более низком уровне, чем была до этого. Причину видят в том, что «… мы так и не смогли переориентировать свой учебный процесс на то, чтобы дети могли использовать полученные знания на практике, – уверена Г. Ковалева. – В ситуациях нетрадиционных наши школьники теряются». Как отмечал Я. Кузьминов, «PISA дает ответ на вопрос, почему, выходя во взрослую жизнь, он [выпускник] становится пассивным избирателем, почему нам так легко навязать любую точку зрения…» [1]. 

Философ М.Мамардашвили считал, что миссия школы концептуализируется как формирование кристаллизованной структуры личности учащегося, превращающей его в устойчивую и самодостаточную единицу, способную связывать причины со следствиями, понимать эту связь. Математика в целом представляет собой «действенное средство» для формирования кристаллизованной структуры личности. Известно мнение, что «математика  –  это доказательство» (Н. Бурбаки). Как отмечал И.Ф. Шарыгин, « … Людьми, понимающими, что такое доказательство, трудно и даже невозможно манипулировать» [2, с. 74].  

В новых образовательных стандартах выдвигается требование сформированности понимания выпускником метапредметных связей и универсальных учебных действий,  в контексте которого выступает идея личностного развития через освоение универсальных учебных действий (компетенций). В рамках такой связи особо остро встает вопрос о том, как должен быть организован процесс обучения математике, чтобы личностное развитие ученика из потенциальной возможности стала реальностью, что предельно актуализируют проблему проектирования социокультурного содержания обучения математике как целостной образовательной системы, включающей совокупность методологических, теоретических, дидактических и инструментально-методических характеристик.  

Напомним, что в ракурсе социокультурной концепции образование определяется как форма человеческой культуры, направленная на трансляцию и усвоение наколенного опыта, знания как носителей культурных ценностей. Выделяется в качестве ведущей категории ценность. Познавательная деятельность личности (учение) рассматривается как феномен культуры, внутренняя динамика освоения ценностей.  

Социокультурное содержание учения в области математики представим как состоящее в усвоении предметных знаний, навыков, умений как форм освоения культурных ценностей, носители которых – математические категории, объекты, методы [3, с. 27]. Отметим, что следует различать понятия «усвоение» (принятие того, что уже создано, накоплено в ходе общественной практики) и «освоение» (не только усвоение, но и преобразование в соответствии со своими целями, потребностями).  

Познавательную деятельность в области математики представим как системное образование, выделяя структурно-функциональные компоненты, которые одновременно могут рассматриваться и как фазы цикла культурного освоения субъектом ценностей (носители которых – математические категории, объекты, методы), как динамику деятельности познания (учения) в области математики: ценностная ориентация, побуждение, адаптация, коммуникация и продуцирование [3, с. 85]. Ценностное отношение как «принятие или отклонение объекта» [4, с. 107] возникает на каждой фазе этого цикла, но, только пройдя все звенья, фазы цикла, становится культурной ценностью. 

В социокультурной парадигме образования качественный учебно-воспитательный процесс должен опираться на мыследеятельностное содержание образования. Что же стоит за этим часто используемым в академической среде термином? Отвечая на этот вопрос, надо начать с того, что в настоящее время в отечественном образовании выделяют три уклада:

• традиционный уклад предметных знаний, умений и навыков,

• инновационный уклад деятельностного и мыследеятельностного образования, 

• информационный уклад ЕГЭ.  

Федеральные стандарты нового поколения ориентируют школу на мыследеятельностное содержание образования, методологические основы которого восходят еще к  Г.П. Щедровицкому: учение – это не взаимодействие человека с окружающей средой, не приспособление к ней, не упражнение и усиление данных от рождения психических функций, не творческий процесс познания объектов окружающего мира, а овладение культурой, накопленной человечеством, перенимание или усвоение фиксированных способов деятельности [3, с. 62].  

В то же время повсеместное внедрение ЕГЭ направлено на формирование информационного уклада. По мере реализации Федеральных стандартов будет происходить определённая «борьба» между мыследеятельностным укладом образования и информационным укладом ЕГЭ.  

Известно, что определённый тип образовательного результата может быть получен лишь на основе соответствующего ему содержания образования. Так, например, основным результатом обучения в советской школе являлся уровень усвоения предметных знаний, умений и навыков именно потому, что это усвоение являлось основным типом содержания образования и соответствовало тем образовательным технологиям, с которыми работал учитель. Здесь следует понимать, что психофизиологической основой образовательных технологий в советской школе являлся бихевиористский подход. Напомним, что бихевиоризм,  используя открытие И.П. Павловым условных рефлексов как основных механизмов работы головного мозга, свел психическую жизнь человека к образованию связей между стимулом и реакцией, а обучение – к приобретению навыков. При этом были сформулированы закономерности образования указанных связей, главная из которых гласит: «Чем чаще предъявляется стимул и следует подкрепление (реакция), тем лучше усвоение». Методика сразу же отреагировала на эти открытия разработкой прямых и непрямых методов обучения, где во главу угла ставилась «дрессура» — многократное повторение упражнений за учителем, запоминание, большей частью механическое, и т.п. [3, с. 64]. 

В этой связи закономерен вопрос: что плохого в том, что ученики путем многократного повторения образцов за учителем смогут усвоить содержательный материал дисциплины, овладеть предметными умениями и навыками? Ответ на этот вопрос заложен, по существу, в основу нашей концепции: подобное обучение опирается на главный критерий «системы всеобуча» – «объем – устная трансляция – зубрежка» информации, которая не понимается, а, следовательно, не усваивается и не применяется, то есть не превращается в знание, – все это унаследованная утопия распредмечивания накопленного «айсберга» человеческой культуры и знания. В то время как суть социокультурной парадигмы – самореализация личности в этой культуре и в этом знании, социализация личности.  

В социокультурной концепции психофизиологической основой деятельностных и мыследеятельностных  образовательных технологий служит теория функциональных систем, разработанная в русле деятельностного подхода П.К. Анохиным [3, с. 65].  

Напомним, что ведущим условием отличия деятельностного подхода от бихевиористского является наличие или отсутствие у обучаемых мотива к осуществлению учебно-познавательной деятельности – положение «Деятельности без мотива не бывает» (А.Н. Леонтьев). Причем совпадение мотива и предмета деятельности является характерным признаком мыследеятельностных образовательных технологий, а формирование мотивации к обучению – важным компонентом в структуре учебной деятельности. Рассмотрим этот вопрос подробнее на примере организации учебой деятельности младших подростков в рамках пропедевтического курса «Основы геометрии» для 5-6 классов. 

Нами разработана технология по формированию деятельности, связанной с усвоением мыслительных умений младших подростков, в рамках пропедевтического курса «Основы геометрии» для 5 – 6 классов. В рамках данной статьи остановимся на формировании умений, способствующих  пропедевтике доказательств геометрических утверждений. При формировании деятельности, связанной с усвоением умений доказывать, учитель в первую очередь сталкивается с проблемой создания мотивации. Возникает проблема формирования у школьников ценностного отношения как принятия достаточно «скучных» положений аксиоматики геометрических пространств в качестве культурной ценности. Здесь акцентируется такой этап динамики освоения ценности, как ценностная ориентация (или рефлексия ценности), складывающаяся из разных форм аналитико-синтетической, поисковой, оценочной и другой познавательной деятельности: поиск смысла идей, заложенных в таких фундаментальных категориях, как, например, доказательство. Трудности вызываются во многом отсутствием понимания необходимости логического доказательства. Школьники видят перед собой очевидное утверждение и не понимают, зачем его нужно еще и доказывать. Так, на вопрос «чем вы занимались на уроке геометрии?» встречаются ответы учеников такого характера: «Учитель нарисовал на доске два равных треугольника и долго доказывал, что они равны». Доказательства первых утверждений воспринимаются формально большинством учеников, причем многие на протяжении всего курса геометрии зазубривают доказательства теорем, не осознавая самой сути доказательства. Поэтому на уровне подготовительного курса геометрии 5 – 6 необходимо формировать у учащихся убеждения в несовершенстве органов чувств, простейших измерительных приборов, показывая, таким образом, ограниченность опытно-индуктивных обоснований. Так, созданный нами пропедевтический курс включает в себя параграф «Как устанавливаются геометрические истины?». В рамках этой темы мы вначале знакомим школьников с методами, используемыми в естественных науках – говорим о наблюдении, опыте, эксперименте. Ставя вопрос о целесообразности применения данных методов в геометрии (и вообще в математике), рассматриваем такие примеры: как экспериментально установить, чему равна сумма углов треугольника; как проверить опытным путем, пересекаются ли параллельные линии? В первом случае школьники, измеряя транспортиром углы треугольника и находя их сумму, приходят к различным значениям, хоть и близким к 180°. Во втором случае учащимся представляется очевидным, что бесконечно продлевать две параллельные линии мы не сможем. Поэтому приходим к выводу, что традиционные для некоторых научных отраслей методы неприменимы в геометрии. 

Раскрывая содержание первого этапа динамики познавательной деятельности – ценностной  ориентации как формирования внутренней мотивации по отношению к субъекту-обучающемуся, отметим, что главным рычагом такой мотивации является интерес к учению, который должен быть заложен не только и не столько в принципах доступности и наглядности, сколько в таких качествах как интересность содержания и процесса учения. Исходя из этого в качестве характеристик разработанной технологии нами выделен тщательный отбор содержания обучения основам геометрии в контексте мировой, национальной культуры, ориентированный на формирование ценностного отношения  –  признание геометрии как ценности, культурного образца, который должен быть передан следующим поколениям. Курс призван обеспечить изменение целевых ориентиров: раскрытие социальной, практической и личностной значимо­сти предметного содержания. В этом смысле ученик, прежде всего, овладевает знаниями о геометрической картине мире, истории развития цивилизации, культуре, целостным восприятием окружаю­щего мира. Что касается объективных предпосылок развития интереса, то можно выделить историчность, которая реализуется посредством введения на уроках культурно-исторического дискурса: вовлечение в процесс изучения собственно математики сведений культурно-исторического ряда – использование объектов, входящих в культурно-историческую зону.  Например, рассматривая значение призм в архитектуре, в качестве примера мы приводим фотографии храмов г. Ельца (рис. 1). При изучении симметрии мы приводим в пример фотографии наличников с окон, сохранившихся в оформлении наших домов.

 

Рис.1. Храм Елецкой иконы Божьей Матери (слева) и Храм введения во храм Пресвятой Богородицы (справа),   г. Елец.

Другие предпосылки развития интереса к учению младших подростков на занятиях геометрией определяется их возрастными особенностями и характером изучаемого материала: преподаваемый материал должен быть достаточно ярким, занимательным. Это условие реализуется нами за счет:

• - использования средств мультимедийной поддержки (геометрические понятия, свойства сопровождаются их динамической интерпретацией - учащимся показываются ролики с анимированными геометрическими объектами);

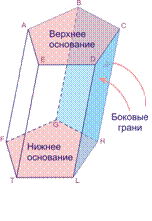
Рис. 2. Получение пирамиды из развертки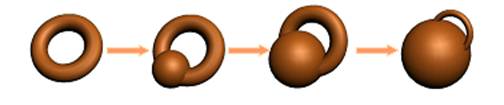

Рис. 3. Пример простейшего гомеоморфного преобразования

Рис. 4. Получение тора вращением окружности

• использования наглядных рисунков, фотографий (например, при изучении призмы и других многогранников и их элементов используются иллюстрации, подобные рис. 5);

• обращения к истории геометрии, этимологии геометрических терминов:

призма – латинская форма греческого слова  «prisma » - опиленная (имелось в виду опиленное бревно); линия - в переводе с латинского “linum” – льняная нить; радиус - в переводе с латинского  "radius" — спица колеса, луч; хорда - в переводке с  греческого – струна; диаметр - в переводе с греческого – диа (“насквозь”), метр (“измерять”) – измерять насквозь.

Рис. 5. Призма

Литература

1. Герасимова Е. Обучение детей на экспорт // Независимая газета. http://www.ng.ru/education/2012-12-25/8_export.html [Дата обращения 15.01.2013].

2. Шарыгин И.Ф. Нужна ли школе ХХI века геометрия?  // Математика в школе, 2004. №4, с. 72-79.

3. Подаева Н.Г. Социокультурная концепция математического образования. – Елец, 2012.

4. Добреньков В.И. Общество и образование  // В.И. Добреньков, В.Я. Нечаев. М.: ИНФРА-М, 2003.

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

_____
 

Natalia G. Podaeva
Doctor of Pedagogical Sciences, Professor of Department of Algebra and Geometry, I.A. Bunin Elets State University, Elets-city
podaeva@mail.ru  

Michael V. Podaev
Candidate of Pedagogical Sciences, Senior lecturer of Department of Mathematical Analysis and Elementary Mathematics, I.A. Bunin Elets State University, Elets-city
podaev86@rambler.ru

Socio-cultural content of school mathematics education: thought-activity technology 

Cognitive activity in the field of mathematics education is presented as a system whose components are considered together, and the phases of the cycle of the cultural development of the subject property: value orientation, motivation, etc. The content of the first phase - the value orientation - for example, thought-activity technology learning the basics of geometry in the 5-6 grades .

Key words:
socio-cultural content of mathematics education, the development of universal educational activities, value orientation, thought-activity content of teaching mathematics; behaviorist approach, the theory of functional systems