Иванова Ольга Александровна
аспирант кафедры методики обучения математики, Российский государственный педагогический университет им. А. И. Герцена, Санкт-Петербург,
olgaal88@mail.ru 

Подходова Наталья Семёновна
доктор педагогических наук, профессор, Российский государственный педагогический университет им. А. И. Герцена, Санкт-Петербург,
podhodova@gmail.com  

Проблемы формирования межпредметных понятий при изучении математики  

Аннотация
Рассмотрены проблемы формирования межпредметных понятий в процессе изучения математики в средней школе. Предложена трактовка межпредметного понятия. Выделены этапы формирования межпредметных понятий.  

Ключевые слова
метапредметные образовательные результаты; metapredmetnye educational results понятие; понятие, подчинённое межпредметному; формирование понятий, логические универсальные учебные действия 

Формирование у учащихся межпредметных понятий является одним из направлений достижения метапредметных образовательных результатов согласно Федеральным Государственным Образовательным Стандартам (ФГОС) второго поколения. Но существует ряд проблем формирования межпредметных понятий. Выделим наиболее существенные из них, решение которых мы рассмотрим в данной статье.

1. В глоссарии ФГОС, методической, философской  литературе нет четкого определения межпредметных понятий.

2. Не выделено отношение между межпредметными и предметными понятиями.

3. Не разработана методика формирования межпредметных понятий, которая должна включать как общую, универсальную часть для разных учебных предметов, так и специфическую для каждого учебного предмета.

4. Не выделена связь между межпредметными понятиями и универсальными учебными действиями. 

Решение первой выделенной проблемы предполагает раскрытие трактовки межпредметного понятия. В математике, в частности, в школьной, чаще всего используется логический подход к трактовке понятия. С точки зрения логики любое понятие может быть охарактеризовано термином (имя, языковое выражение, знак понятия), смыслом (способ, которым может быть задано понятие) и значением (тот реальный предмет, который обозначен термином понятия) [1]. Связь между термином, смыслом и значением может быть представлена в виде семантического треугольника Фреге (рис .1)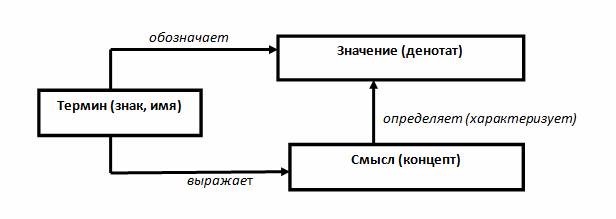

 

Рис. 1. Семантический треугольник Фреге

Рассмотрим, например, понятие, обозначенное термином «Пётр I». Значением этого понятия будет конкретный человек, носивший это имя. А смыслов может быть несколько –  «первый император Российской империи», «создатель военного флота  России», «основатель города Санкт-Петербург». Рассмотрим пример математического понятия. Так, для термина «квадрат» значением является некий идеальный объект, который можно представить или нарисовать. Значениями математических понятий всегда являются идеальные объекты. Смысл математических понятий может быть передан определением, системой аксиом, признаком, описанием свойств объектов, существенных для понятия. У понятия «квадрат» может быть несколько смыслов: «прямоугольник с равными сторонами», «правильный четырёхугольник», «ромб с равными углами». Изучение понятий в методике обучения математике связано с рассмотрением таких характеристик понятия, как объём и содержание. Объём – множество объектов, выделяемых и обобщаемых в понятии. Содержание – совокупность свойств объектов, существенных для понятия. С логической точки зрения объем понятия фактически представляет множество его значений, а содержание  отражает смыслы понятия. Как же можно охарактеризовать межпредметное понятие в рамках логики? 

Рассмотри предметные понятия, термин или часть термина которых совпадает. Например, понятия «система уравнений», «система отсчёта», «кровеносная система», «система правления» имеют общую часть в названии - «система», а также  пересечение их смыслов или содержаний не пусто (понятия имеют общие свойства). А вот значения их не совпадают, т.е. объемы этих понятий не пересекаются  (не имеют общих элементов). Такие понятия в логике определяют как соподчиненные.  Их общий смысл и образует смысл или содержание межпредметного понятия, а все значения этих понятий образуют значения или объем межпредметного понятия.  

Изобразим отношения  между  соподчинёнными понятиями  с  помощью  кругов Эйлера, где каждый круг  обозначает объём понятия (рис. 2.).

Рис. 2. Отношение между соподчинёнными понятиями по объёму 

Отношение между соподчинёнными понятиями по содержанию можно также изобразить с помощью кругов Эйлера (рис. 3.).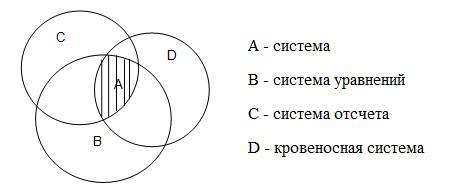

Рис. 3. Отношение между соподчинёнными понятиями по содержанию 

Определенные таким образом межпредметные понятия не являются предметной целью изучения математики, да и большинства учебных предметов. Целью изучения на разных предметах являются понятия, подчиненные межпредметному и соподчиненные между собой. Поэтому вряд ли целесообразно формирование межпредметного понятия как собственно понятия, да и это достаточно сложно в рамках одного предмета, а вот обобщенное представление (предпонятие по Выготскому Л.С. [2], как  переходная ступень от мышления в образах к мышлению в понятия) необходимо. Ведь именно межпредметные понятия в том смысле, что мы определили выше, являются основой интеграции предметных понятий, позволяют избежать обособленности предметных знаний, способствуют формированию целостной системы знаний. Поэтому необходимым условием создания целостной картины мира является формирование у учащихся обобщенного представления о межпредметном понятии как интегрирующего понятия, и уже на этой основе формирование подчиненного ему предметного понятия. Обобщенное представление включает различные образы (образуют объем понятия) и свойства, существенные для межпредметного понятия (образуют содержание понятия), т.е. «картинки понятия» плюс свойства, существенные для понятия. Запас образов понятия у учащихся должен быть достаточно широк. Ведь в  работе с понятиями, при решении задач учащиеся, в основном, опираются на образы объектов, что требует сформированности достаточно широкого объёма понятия. В противном случае могут возникать такие ситуации: учащиеся, зная определение геометрической прогрессии, не распознают ее в задаче; рассматривая пианино с плоскими поверхностями учащиеся, да и учителя часто не узнают в нем модель призмы. 

Определив, что мы понимаем под межпредметными понятиями, рассмотрим возможные пути их формирования в процессе обучения. 

Нами были выделены этапы формирования межпредметных и подчинённых им понятий. Этапы распределены по двум блокам: первый выполняется учителем при подготовке к урокам,  второй реализуется непосредственно на уроках. Раскроем эти этапы, рассмотрев их реализацию на примере понятия «функция». Частота употребления этого термина составляет  1825 раз на ≈ 300 миллионов слов, то есть  каждое 165 слово в нашей речи – это слово функция. Учащиеся часто употребляют в речи термин «функция», имея в виду  действие, выполняемое человеком или предметом. Также данный термин встречается в учебниках по различным предметам. Например, функция денег (обществознание), функция опорно-двигательного аппарата (биология). А в курсе алгебры понятие «функция» является важнейшим изучаемым понятием.  

I блок этапов.
I  этап. Выделение понятий, соподчинённых изучаемому на уроках математики понятию и рассматриваемых на других учебных предметах.

Этап реализуется на основе  анализа содержания других учебных предметов. На уроках математики изучается «числовая функция», на других предметах: «функция органов дыхания, печени», «функция государства»,  «функции членов предложения» и т.д. Все эти понятия подчинены межпредметному понятию «функция». 

II этап. Построение обобщенного представления о соответствующем межпредметном понятии. 

На основе анализа трактовок выделенных на первом этапе соподчиненных понятий:

• рассматриваются различные значения (образы) соподчинённых понятий, они образуют объем межпредметного понятия,

• выделяются свойства, существенные для вводимого понятия; они образуют содержание межпредметного понятия,

• рассматриваются всевозможные значения понятия (объем понятия),

• проверяется выполнение выделенных свойств для подчиненного математического понятия.

В словарях и учебниках встречаются более 10 различных трактовок понятия «функция». Проведённый анализ этих трактовок позволил выделить два основных смысла этого понятия: 1) о функции мы говорим как о действии, выполняемом кем-либо или чем-либо, назначении человека или предмета; 2) под функцией понимается соответствие между элементами двух множеств, при котором изменение элементом в одном множестве влечёт изменение элементов в другом множестве. При этом природа элементов этих множеств может быть любой [3]. 

Как показал проведённый нами эксперимент, при ответе на вопрос  «что такое функция» 55% учащихся 7-8 классов на уроках математики и до 90% на уроках  других учебных предметов под функцией понимают действие. Причем почти половина остальных учащихся на уроках математики в качестве определения функции предлагали конкретные функции, заданные аналитически, или их графики, т.е. фактически описывали часть объема понятия, а не содержание, что требует определение понятия. В данной ситуации можно поступить по-разному: 

1. Не связывать «математический» объективный смысл понятия «функция» с объективными смыслами в других науках и субъективным смыслом ребёнка, формировать понятие «числовая функция» в традиционном ключе.

2. Развести разные термины соподчиненных понятий,  не выходя на межпредметное понятие и не показывая детям, что смыслы этих соподчиненных понятий    имеют общее.

3. Установить связь между различными смыслами понятий.

Оптимальным для достижения метапредметных результатов является третий путь.  Как его реализовать? 

В жизни, рассматривая функцию, мы выделяем только одно множество - множество действий. А понимание функции во втором смысле предполагает выделение двух множеств.  Значит, эти две трактовки противоречивы? Если их проанализировать их, то, оказывается, что противоречия нет. Никакое действие не существует без объекта, который выполняет это действие. Поэтому, рассматривая функцию вне математики, можно выделить и второе множество, заданное неявно, – множество объектов, которые обладают этими функциями (или совершают эти действия). Недаром вне математики говорят о функциях чего-то или кого-то, например, функции членов предложения, функции органов пищеварения. Да и в математике функцию рассматривают заданную на каком-либо множестве и часто описывают через определенное аналитическое выражение.  

Непротиворечивость трактовок подтверждает и история развития математики. На определённом историческом этапе под функцией понималась только зависимая переменная, то есть объем понятия был представлен только одним множеством. После введения термина «функция» в математике в 1673 году Готфридом Вильгельмом фон Лейбницем и до второй половины XIX века в определении функции этим термином обозначалось только одно множество (переменную величину у называли функцией переменной величины х). В связи с необходимостью описания вновь открытых законов природы понятие «функция» уточнялось и обобщалось. И только после введения понятия множества во второй половине XX века, была дана современная трактовка понятия «функция», в которой функция рассматривается как соответствие (особое) между множествами любой природы.   

Таким образом, понятие функции в математике и вне ее имеют общие свойства, а именно наличие двух множеств и определенная связь между ними. 

 III этап. Выделяются свойства, специфичные для математического понятия, подчиненного межпредметному. 

II блок этапов.

IV этап. Выявление субъектного опыта учащихся 

Этот этап реализуется уже непосредственно на уроке. Он необходим для выявления субъективного смысла (житейского представления) межпредметного понятия у каждого ученика и установления на этой основе связи с вводимым понятием. Любое понятие  в сознании человека представлено в виде определенного семантического поля, которое связывает разные смыслы понятия [4]. Поэтому называние знакомого термина актуализирует у ребенка это поле и определенный смысл, который ребенок связывает с названным термином. На этот смысл и будет опираться ребенок при формировании понятия в силу определяющей роли субъектного опыта в восприятии и усвоении информации. Но этот житейский смысл не всегда совпадает с научным смыслом понятия. Поэтому необходимо выявить житейский смысл понятия, и  в дальнейшем либо опираться на него, либо в случае расхождения с научным смыслом организовать деятельность, в которой у учащихся будут сформированы образы, адекватные формируемому понятию.  

Впервые термин «функция» встречается в учебнике природоведения 5 класса при изучении функций растений и животных. Здесь функция понимается как действие, выполняемое растениями и животными. В таком же смысле можно понимать функции государства на уроках обществознания, функции внутренних органов и различных тканей организма на уроках биологии, функцию в бытовом значении. Как показало проведенное исследование, именно в этом смысле понимают многие учащиеся функцию даже после знакомства с определением в алгебре («работает» определяющая роль субъектного опыта). При выполнении задания назвать словосочетания со словом «функция», большинство учащихся называли функции мобильного телефона, бытовых приборов, растений. Поэтому введение математического понятия целесообразно начать именно со значений функций, знакомых ребенку.  

V этап.  Формирование у учащихся обобщённого представления (предпонятия) о межпредметном понятии. 

На этом этапе происходит знакомство учащихся с разными значениями (объемом) межпредметного понятия и разными его смыслами через определенную систему заданий. Можно предложить учащимся, перечислить функции бытовых приборов и записать их в столбик. Но так как эти функции выполняют определенные приборы, то целесообразно записать их названия в другой столбик левее первого. Далее обсудить, что, например, функцией стиральной машины вряд ли является подогрев продуктов, а холодильника – стирка белья. То есть существует определенная связь  между элементами первого и второго столбца, правило, по которому элементам первого столбца (множества) ставятся в соответствие элементы второго столбца (множества). 

Или, учащимся можно предложить задания, в которых требуется установить соответствие  между множествами, соединив стрелкой соответствующие элементы, и дать названия множествам:

нервная ткань	обеспечивает сокращение, а затем расслабление сердечной мышцы,
костная ткань	восприятие, переработки, хранения и передачи информации, поступающей из окружающей среды и от органов самого организма
сердечная ткань	опорная функция

Учащиеся под функцией понимают элементы множества, записанного во втором столбике (множество действий, которые выполняют клетки определенной ткани организма). Но никакое действие не существует без объекта, который выполняет это действие. Поэтому можно выделить второе множество, которое неявно задано – множество мобильных телефонов (множество видов тканей организма) и правило соответствия между этими множествами. Но функция – это не только соответствие между элементами двух множеств, но ещё и зависимость. В приведённых выше примерах сложно сказать однозначно, элементы какого из множеств являются зависимыми от элементов другого множества. Поэтому  целесообразно предложить задание, в котором можно выделить зависимые и независимые переменные. Например, предложить учащимся установить соответствие между величиной пути, пройденным автомобилем при постоянной  скорости автомобиля, равной  60 км/ч,  и временем, за которое пройден этот путь. 

Путь, км/ч	Время, ч
60 120 150	2,5 1 2

Далее учащимся целесообразно предложить ответить на вопрос, какая из величин от какой зависит. Из каких элементов состоит множество зависимых переменных? независимых?  

Цель предложенных выше заданий – сформировать обобщенный образ понятия функции на основе уже имеющихся  у учащихся представлений о функции, который может быть представлен схемой (на рис.4а или рис.4b), и выделить свойства, существенные для межпредметного понятия: наличие двух множеств и связи между ними. Рисунок 4b предложен для того, чтобы показать учащимся, что элементы множеств могут быть расположены по-разному: в таком положении они встретятся с функциональной зависимостью, заданной графически.

 

Рис. 4. Образ межпредметного  понятия  «функция» 

VI этап. Демонстрация специфики понятия данной предметной области, подчинённого межпредметному, связи его с другими учебными предметами. Введение определения предметного понятия, подчиненного предметному. Запись определения в алгоритмизированном виде.  

Перечисленные этапы носят универсальный характер, могут быть использованы в методике обучения разным учебным предметам. А вот VI этап будет включать разные подэтапы, отражающие специфику методики учебного предмета и формируемого предметного понятия. 

В рамках системно-деятельностного подхода согласно ФГОС предполагается, что к теоретическому выводу ребенок приходит в результате собственной деятельности. Это значит, что к определению функции (содержанию понятия) учеников целесообразно подвести через решение задач, которые знакомят с объемом понятия, а именно с различными конкретными представителями – функциональными зависимости (кусочно-заданной функцией; функцией, заданной на множестве натуральных чисел; непрерывной функцией) и разными способами их задания (таблица, график, словесный способ и аналитический), а также позволяют выделить специфичные для математики свойства функции. Это позволит избежать формирования у учащихся представления о функции только как аналитического выражения или графика в виде непрерывной линии. 

В ФГОС выделены такие познавательные логические УУД, как выделение свойств, существенных для понятия, умение определять понятие. Их формированию будут способствовать индуктивный способ введения понятия (описанный выше) и запись определения в виде алгоритма, где четко выделены все свойства, существенные для понятия (как общие, присущие понятиям, соподчиненным межпредметному, так и специфичные) (рис. 5).

Рис. 5. Определение понятия функция

Родовое понятие в определении целесообразно подчеркнуть. Введение элементов логики в рамках ФГОС предоставляет возможность при работе с определением показать связь между родовым понятием и видовыми отличиями, которую можно изобразить знаком системы, отразив конъюнктивную связь между родовым понятием и видовыми отличиями. Работа с такой  записью способствует формированию такого логического УУД как отнесение объекта к понятию. 

Но есть еще группа  межпредметных понятий, связанных непосредственно с универсальными учебными действиями (УУД), даже в отношении термина. Это, например, познавательные УУД: классификация, сравнение, моделирование и т.д. Их название  фактически отражает термин соответствующего межпредметного понятия. Эти понятия имеют одинаковый смысл для большинства учебных предметов, определены  вне учебных предметов и частично уже описаны  [5]. Так, для многих логических УУД соответствующие понятия определены в логике, но некоторые имеют специфику в рамках учебного предмета, например, сравнение как уподобление имеет место в литературе, но не используется в математике. Их формирование может реализоваться в разных предметах  приблизительно одинаково, но на разном содержании, внепредметном и предметном,   с демонстрацией, как их универсальности, так и специфики, если она присутствует.

Литература

1. Фреге Г. Логика и логическая семантика. - М.: Аспект Пресс, 2000.

2. Выготский Л.С. Лекции по педологии. Ижевск, Издательство Удмуртского университета, 2001.

3. Математический энциклопедический словарь. /Гл. ред. Ю.В. Прохоров; – М.: Сов. Энциклопедия, 1988.

4. Лурия А.Р Мозг и психические процессы. — М., 1963, Т.1; М., 1970. Т.2.

5. Подходова Н.С. Особенности формирования познавательных  универсальных учебных действий. //Метаметодика как перспективное направление развития предметных методик обучения: сборник научных статей. Выпуск 9.  - СПб.       Изд-во «Статус», 2012.   

Рекомендовано к публикации
Н.Ф.Радионова, доктор педагогических наук, член Редакционной Коллегии

_____

Olga A. Ivanova
Postgraduate student, Department of mathematics teaching methods, Al.Herzen State Pedagogical University of Russia, St. Petersburg
olgaal88@mail.ru  

Natalia S. Podhodova
Doctor of Pedagogical Sciences, Professor, Department of mathematics teaching methods, Al.Herzen State Pedagogical University of Russia, St. Petersburg
podhodova@gmail.com  

Problems of formation of interdisciplinary concepts in the study of mathematics 

This article considers the problem of formation of interdisciplinary concepts in the study of mathematics in secondary school. Proposed interpretation of the concept of cross-curriculum; Stages of formation of interdisciplinary concepts.

Keywords:
metapredmetnye educational results, intersubject concept, the concept of subordinate cross-curriculum, the formation of concepts, universal logic training actions