Чибичян Марина Семеновна
соискатель по кафедре методики обучения математике Российский государственный педагогический университет им. А.И. Герцена,  Санкт-Петербург
margo-m@bk.ru  

Модель реализации адаптивных тестов по алгебре и началам анализа 

Аннотация
В статье рассматривается проблема организации контроля знаний учащихся с использованием адаптивных тестов. Обосновывается выбор показателей, на основании которых группируются задания в адаптивном тесте. На примере темы «Логарифмическая функция» задается модель реализации адаптивных тестов, называемая пирамидальной, по которой описывается механизм осуществления адаптации при проведении тестов. 

Ключевые слова
адаптивные тесты, сложность тестового задания, форма представления информации, модель реализации адаптивных тестов 

Проблема эффективной организации контроля знаний учащихся актуальна всегда, когда осуществляется очередной виток реформирования образования, будь то парадигма, будь то технологии, будь то образовательные стандарты. В настоящее время преобладает тестовая форма контроля, что предполагает разработку содержания и технологии использования данной формы. Развитие компьютерных технологий расширяет возможности тестов как современной формы контроля и оценки знаний.  

Компьютеризация контроля и активное развитие тестовых технологий привело к возникновению так называемых адаптивных тестов. Острая потребность в совершенствовании процесса тестирования, в повышении его эффективности путем немедленного реагирования на индивидуальные особенности подготовки испытуемых в процессе предъявления заданий обуславливает необходимость разработки адаптивных тестов. Теоретические и практические аспекты проблемы компьютеризации контроля и адаптивных тестов исследовались и продолжают исследоваться многими учеными. Однако анализ работ в области преподавания математики выявил, что нет ни одного исследования, напрямую связанного с адаптивными тестами по алгебре и началам анализа, что позволяет говорить об актуальности проблемы нашего исследования, которая заключается в научном обосновании и реализации адаптивных тестов на уроках алгебры и начал анализа в старших классах.  

Любой адаптивный тест строится на основной идее выстраивания линии усложнения заданий. Однако помимо уровня сложности, задания в адаптивном тесте можно сгруппировать на основе других показателей. Эти показатели были уже представлены в нашей работе [1, с. 466 – 468]. Мы предлагаем рассмотреть в качестве второго показателя – форму представления информации в заданиях:

• вербальную, с использованием словесных формулировок;

• графическую, где условие представлено посредством графиков;

• аналитическую, с использованием формул и аналитических выражений.

Выбор данного показателя обуславливается несколькими причинами. Во-первых, содержание курса алгебры и начал анализа 10 – 11 классов, позволяет использовать задачи, информация в которых представлена в различных формах. Во-вторых, данные констатирующего эксперимента, указывают на то, что при решении задач очень важным является форма представления информации в ней. В некоторых случаях успешность выполнения задач одного содержания и уровня сложности, зависела от формы представления информации в ней. 

Многие задачи содержат требование выполнить то или иное действие логического характера: доказать, обосновать, определить, расклассифицировать, сделать вывод. При этом форма представления информации в таких задачах может быть вербальной или аналитической. 

Пример (вербальная форма).

Доказать, что синус суммы двух внутренних углов треугольника равен синусу его третьего угла. [2, с. 159] 

Пример (аналитическая форма).

Доказать:

[1, с.158] 

Изучение алгебры и начал анализа дает возможность для развития алгоритмических знаний, умений и навыков. И нас в первую очередь будет интересовать умение действовать по знакомому и незнакомому алгоритмам. Стандартные формулировки таких заданий: вычислить, сравнить, решить уравнение (неравенство), упростить и т.д. Такие задачи могут быть представлены как в вербальной и аналитической, так и в графической форме: 

Примеры (вербальная форма)

При каких значениях  имеет смысл выражение:

? [2, с.22] 

Пример (аналитическая форма)

Вычислить . 

Наконец, необходимое для изучения теории обилие графиков, которое определяется многообразием изучаемых функций и их свойств, предоставляет возможность для развития элементов графических знаний, умений и навыков: умения выполнять различные действия с графиками, преобразовывать информацию к графическому виду и обратно и др. Форма представления таких заданий может быть графической, аналитической и вербально. Благодаря компьютерным технологиям появились большие возможности для развития графических знаний, умений и навыков с использованием тестов. 

Пример (вербальная форма)

Какое преобразование переводит график функции  в . 

Пример (графическая форма)

Используя график функции , найти ее точки экстремума (при этом сам график задан) 

Итак, выделены направления, которые будут использоваться при создании адаптивных тестов:

• уровень сложности математических задач, к решению которых подготовлен учащийся;

• форма представления информации в заданиях (графическая, аналитическая или вербальная).

В настоящее время существуют три варианта формирования адаптивного теста. Первый – пирамидальный, когда без предварительной оценки, каждому учащемуся дается задание средней сложности и затем, в зависимости от ответа, формируется следующее задание, шкала трудности которого ниже или выше в 2 раза. Второй способ (flexilevel) в начале использует любой уровень сложности, постепенно подбирая подходящий для данного учащегося. При третьем стратификационном способе (stratified adaptive) задания берутся из банка заданий, разделенных по уровням сложности. При правильном ответе следующее задание берется из верхнего уровня, при неправильном – из нижнего [3].  

Опишем механизм «адаптации», осуществляемый при переходе к следующей задаче. Мы будем пользоваться первой моделью реализации адаптивных тестов, «пирамидальной». Каждому учащемуся в начале выдается задание среднего уровня сложности, далее, в зависимости от ответа формируется задание, шкала сложности которого выше или ниже. Эта модель позволит избежать длительного пути прохождения к заданиям своего уровня, как в случае со второй моделью, когда в начале выдается задание произвольного уровня сложности. И если знания учащегося на 1 уровне, а ему сразу выдается задание 3 уровня, то необходимо пройти и второй уровень, прежде чем дойти до своего. С другой стороны, мы не воспользовались третьей моделью, когда при правильно ответе следующее задание берется из верхнего уровня, при неправильном – из нижнего, чтобы избежать постоянных переходов из уровня в уровень, когда учащийся часто ошибается. 

Итак, учащийся начинает выполнение адаптивного теста с задания второго уровня сложности. Здесь возможны два случая:

• выполнил задание верно;

• выполнил задание неверно.

В первом случае, повышаем уровень сложности следующего задания (если это возможно).

Во втором случае (т.е. после неверного выполнения задания), ему выдается прямая подсказка в виде решенного данного примера. После чего повторно предлагается аналогичная задача. Если после этого учащийся выдает правильный ответ, то уровень следующего задания не меняется, если неправильный, то уровень понижается. Данная схема выполняется на каждом этапе прохождения адаптивного теста. 

Приведем пример функционирования адаптивного теста из подтемы «Определение и свойства логарифмов».

Тест начинается с заставки:

1 шаг. Выдается всем тестируемым задание второго уровня сложности: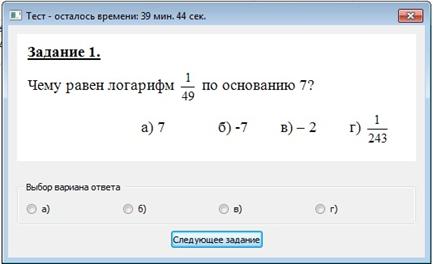 

2 шаг. При условии верного выполнения задания, уровень сложности следующего задания повышается, т.е. выдается второе задание третьего уровня сложности.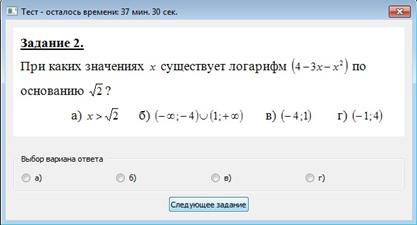

2’ шаг. При неверном выполнении задания предъявляется подсказка в виде верного решения: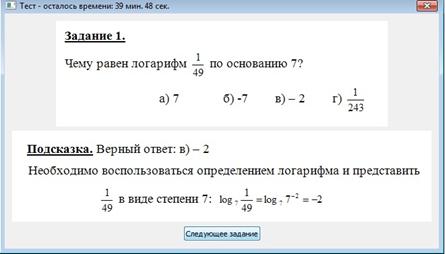

3’ шаг. Предлагается еще одно аналогичное дополнительное задание: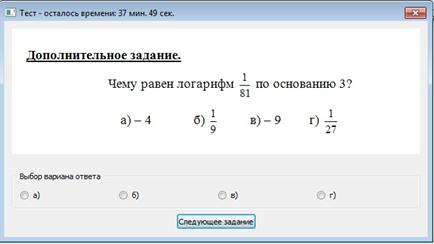

4’ шаг. Справился с дополнительным заданием – выдается следующее задание (не аналогичное) того же уровня сложности: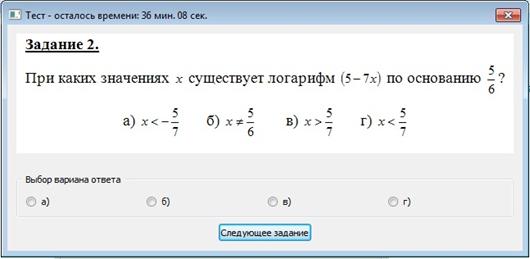

5’ шаг. Не справился с дополнительным заданием – выдается следующее задание (не аналогичное) меньшего уровня сложности:

В конце прохождения теста на экране появляется таблица результатов выполнения теста следующего вида: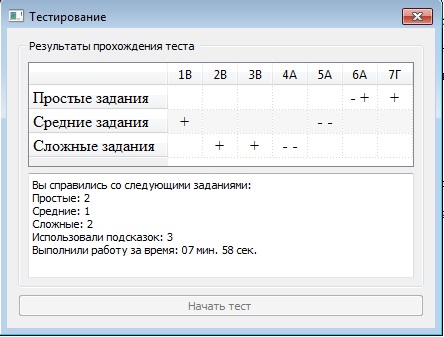

Знак «+» означает, что задание выполнено верно с первого раза, без подсказок; «– +» означает, что само задание выполнено неверно, но дополнительное задание, после предъявления подсказки, выполнено верно; «– –» ни само задание, ни дополнительно не выполнены верно. 

По данной таблице можно судить, во-первых, об уровне сложности заданий, с которыми справился учащийся, во-вторых, выявить задания, с предпочтительной формой представления информации в условии. Таким образом, полученный профиль задает основания для дальнейшей коррекции и выбора направления работы с каждым учащимся. Данные обучающего эксперимента подтверждают эффективность использования адаптивных тестов при обучении алгебре и началам анализа. 

Литература:

1. Чибичян М.С. Конструирование адаптивных тестов для изучения курса алгебры и начал анализа // Вестник Орловского Государственного Университета / Серия: новые гуманитарные исследования, № 6 (20), ноябрь – декабрь, 2011. с. 466 – 468.

2. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра и начала анализа: учеб. для 10 – 11 кл. общеобразоват. учреждений. – 13-е изд. – М.: Просвещение, 2005.

3. Гусева А.И. Адаптивные методики тестирования. – М.: МИФИ, 2002

Рекомендовано к публикации:
В.И. Снегурова. доктор педагогических наук, научный руководитель работы
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегши

_____ 

Marina S. Chibichyan
Applicant of the Department of methodology of teaching mathematics, Al.Herzen State Pedagogical University of Russia, Saint-Petersburg
margo-m@bk.ru  

The model of the implementation of adaptive tests of algebra and calculus

The article considers the problem of the organization of the control of knowledge of students using adaptive tests. The choice of the indicators, on the basis of which the specific job in adaptive test. On the example of «Logarithmic function sets the model for the implementation of adaptive tests, called pyramid, which describes the mechanism of implementation of adaptation when conducting tests.

Key words:
adaptive tests, the complexity of the test, form of information representation, the model of the implementation of adaptive tests