Ларченкова Людмила Анатольевна
кандидат педагогических наук, доцент, кафедра методики обучения физике, Российский государственный педагогический университет
им.  А. И. Герцена, Санкт-Петербург
larludmila@yandex.ru  

Долженко Елена Васильевна
учитель физики, лицей № 369 Красносельского района Санкт-Петербурга, соискатель по кафедре методики обучения физике, Российский государственный педагогический университет им. А.И.Герцена, Санкт- Петербург,
kvark0308@mail.ru  

Использование универсальности математических моделей при обучении решению физических задач в средней школе

Аннотация:
в статье обсуждаются методические возможности обучения элементам математического моделирования при решении физических задач в обучении физике в средней школе на примере универсальности математических моделей.

Ключевые слова:
обучение решению физических задач, математическое моделирование реальных явлений, универсальность математических моделей

В государственном образовательном стандарте по физике умение моделировать отнесено к общеучебным умениям. В методической литературе моделированию уделяется большое внимание. Исследователи в области методики обучения физике под моделированием понимают вид учебной деятельности, который включает в себя построение моделей или выбор готовых и изучение их с целью получения новых сведений о физических объектах [1-3]. В содержание термина «модель» они вкладывают тот же смысл, что и физики, поскольку типичные математические модели в физике выражают фундаментальные законы природы, проявляющиеся в конкретных ситуациях. Но, как правило, рекомендации по обучению учащихся моделированию сводятся к сообщению информации об идеализированных объектах изучаемых физических теорий и об идеализации условий, в которых протекает физическое явление. Однако моделирование не может быть освоено посредством прямых указаний («а теперь мы будем моделировать» и т.д.), а должно быть развернуто в процессе обучения в виде особой деятельности, что на практике представляет собой большую проблему.

Обучение математическому моделированию подразумевает не просто усвоение определенных правил и способов действия, а именно развитие своеобразного стиля мышления, отличного от того, который формировался при «классическом» подходе к изучению естественных и гуманитарных наук, в связи с чем особую актуальность имеет поиск соответствующих средств обучения. В этих условиях обращает на себя внимание такое средство как учебные физические задачи, методический потенциал которых еще не изучен до конца и полностью не исчерпан. Именно физические задачи позволяют, подчеркивая самые принципиальные аспекты математического моделирования, вырабатывать необходимые для этого навыки. Фактически при решении любой физической задачи, поставленной таким образом, что она описывает реальные объекты, а не идеализированные понятия (тело, материальную точку, абстрактную волну и т.д.) приходится прибегать к математическому моделированию. При этом устанавливается, какие физические законы описывают исследуемую систему, какие приближения могут быть сделаны в процессе решения задачи, какие идеализированные понятия целесообразно использовать при написании уравнений, чем и на каком основании можно пренебречь [4].

Если рассматривать моделирование как ведущую идею решения физических задач, необходимо остановиться на таком важном аспекте, как свойства математических моделей, основными среди которых  считают следующие [5]:

1. Адекватность предполагает воспроизведение моделью с необходимой полнотой и точностью всех свойств объекта или явления, существенных для целей данного исследования.

2. Простота предполагает соответствие количества учитываемых факторов, возможностей имеющегося математического аппарата и задач проводимого исследования.

3. Оснащенность предполагает принципиальную возможность получения интересующих утверждений с помощью выбранных математических методов.

4. Продуктивность предполагает возможность получения с помощью модели новых знаний об исследуемом объекте.

5. Устойчивость предполагает, что  малое изменение параметров и функций, описывающих модель, не должно влиять на результат исследования.

6. Наглядность предполагает возможность выявления определенного содержания  даже при первичном знакомстве с построенной математической моделью, что позволяет сразу же наметить план решения задачи и даже предсказать  результат решения. 

7. Универсальность предполагает возможность применения одной и той же модели к объектам принципиально различной природы.

8. Иерархичность предполагает возможность описания явлений с помощью    моделей, различающихся по степени полноты, адекватности и простоты, которые могут быть обобщены, структурированы и упорядочены в определенную последовательность.  

На первый взгляд может показаться, что все свойства математической модели являются необходимыми следствиями исходно предусмотренных, явно оговоренных свойств реального объекта. Однако, при решении задач указанные свойства математических моделей тесно переплетаются и не всегда очевидны для учащихся. Более того следствия, получаемые с помощью математических моделей, могут быть не очевидны и осознаны не сразу, что проявляется не только в обучении, но характерно и для настоящих научных исследований. Так, например, Г. Герц писал о неисчерпаемости теории Максвелла: «Нельзя изучать эту удивительную теорию, не испытывая по временам такого чувства, будто математические формулы живут собственной жизнью, обладают собственным разумом – кажется, что эти формулы умнее нас, умнее даже самого автора, как будто они дают нам больше, чем в свое время было в них заложено» ([цит. по [6, с.161]). В то же время следует понимать, что математика не обязательно говорит истину о реальном мире. Природа не предписывает и не запрещает никаких математических теорий. Теоретическая физика не может не опираться на физические аксиомы, например, такие, как закон всемирного тяготения, которые могут рассматриваться в качестве обобщения опыта, но подобные обобщения могут быть не свободны от ошибок. С другой стороны, математический аппарат нередко гораздо лучше выдерживает испытание временем, нежели те физические представления, которые он изначально выражал. Ж. Фурье разработал полную и подробную математическую теорию теплопроводности, в которой теплота рассматривалась как некий флюид. Эта теория уже давно отброшена и забыта, но предложенный Фурье математический аппарат и поныне находит широкое применение в акустике и других областях физики [6]

Остановимся подробнее на возможности использования свойства универсальности математической модели, что является показателем ее высокого качества и дает возможность рассматривать физическую ситуацию в целом, осуществлять обобщение знаний из разных областей физики, обосновывать единство физических законов, т.е. позволяет в единичном видеть общее и с позиций общего оценивать особенное. Наше исследование показывает, что возможность получения далеких следствий с помощью математических моделей, построенных для анализа различных конкретных ситуации, доступна даже при решении учебных физических задач в средней школе. Кроме того, на основе универсальности математических моделей, может быть построена методическая работа по преодолению психолого-познавательного барьера между учебными дисциплинами физики и математики, который является одной из причин низкой мотивации и успеваемости учащихся при изучении физики [7]. Такими универсальными моделями являются линейная и квадратичная функции, пропорция, квадратное уравнение, соотношения сторон и углов в треугольниках, тригонометрические функции, система линейных уравнений, уравнение гармонического колебания, формулы сокращенного умножения и т.д. Универсальным является подход к рассмотрению явлений, возникающих при переходе физической системы из одного состояния в другое, если не требуется детализация самого процесса перехода (применение законов сохранения, газовых законов осуществляется по принципу «было-стало»). Осознание учащимися универсальности математических моделей может способствовать преодолению познавательных затруднений и нахождению решения проблем в нестандартной ситуации.

В качестве примера приведем ряд задач, в которых требуется выяснить зависимость периода колебаний какой-либо системы от ее параметров в случаях, когда природа ее колебаний определяется не только простыми механическими процессами, но и процессами иной природы. При известной условности модели можно считать, что в таких системах возникают колебания, описываемые известным уравнением

В процессе решения ряда таких задач в рамках школьной физики достаточно получить выражение для силы (различного происхождения), которую при известных допущениях можно считать квазиупругой, или в случае замкнутой системы и отсутствия диссипативных сил воспользоваться законом сохранения энергии.

Приведем примеры таких задач:

1. С какой частотой будет колебаться бутылка массой m с площадью поперечного сечения S, плавающая на поверхности воды
   в вертикальном положении? Сопротивлением воды пренебречь.

2. Представьте себе, что сквозь Землю по диаметру прорыли сквозную шахту. Опишите характер движения тела, брошенного в шахту, пренебрегая вращением Земли и сопротивлением движению.

3. На двух вращающихся в противоположные стороны валиках лежит горизонтально однородная доска. Расстояние между осями валиков l. Коэффициенты трения между доской и валиками одинаковы и равны m. Определить период колебаний доски (см. рисунок ниже)

4. В сосуде, разделенном подвижным поршнем массы m и площадью поперечного сечения S, находится идеальный газ. Когда поршень расположен ровно посередине сосуда, давление в каждой половине p, объем половины сосуда равен V. Определите период малых колебаний поршня, считая процесс изотермическим. Трением пренебречь.

5. Бусинка, имеющая заряд q и массу m, может скользить без трения вдоль вертикально расположенной  непроводящей спицы, в нижней части которой закреплен точечный заряд Q. Найти период малых колебаний бусинки вокруг положения равновесия.

6. Пружинный маятник массой m (металлический стержень, подвешенный на двух пружинах) дополнен электрической схемой. Между верхними концами проводящих пружин жесткостью k «включен» конденсатор емкостью С. Образовавшийся замкнутый контур помещен в однородное внешнее магнитное поле. Вектор магнитной индукции В перпендикулярен плоскости контура. Считая активное сопротивление контура и индуктивность пружин равными нулю, определить период малых колебаний стержня. При колебаниях стержень остается горизонтальным.

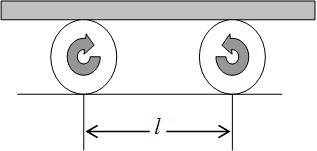
Решения этих задач известны, поэтому останавливаться на них не будем. Более интересным в связи с использованием универсальности математических моделей является следующий сюжет.

Задача. Санки массой m и длиной L скользят по гладкому льду со скоростью v. Неожиданно лед заканчивается, и санки въезжают на асфальт, после чего они останавливаются, заехав на асфальт лишь на ¾ длины. Коэффициент трения санок о лед равен m. Найти время торможения санок.

Нетрудно видеть, что торможение санок происходит под действием силы трения скольжения, величина которой меняется в процессе движения по линейному закону. Тогда уравнение движения в проекции на направление движения имеет вид:

откуда видно, что вторая производная от координаты а_х пропорциональна самой координате, взятой с противоположным знаком, что соответствует общему виду уравнения гармонического колебания:

в котором для данного случая

Несмотря на парадоксальность результата – ведь в описанной ситуации санки никаких колебаний не совершают, а двигаются замедленно до полной остановки, представления об универсальности математической модели позволяют получить ответ на вопрос задачи. При гармоническом колебании в механических системах скорость изменяется от максимального значения до нуля за ¼ периода, следовательно, и в данном случае искомое время может быть найдено как

Следует дополнительно отметить, что приведенное условие задачи содержит данные, не вошедшие в ответ, что дает возможность продолжить работу с математической моделью для анализа физической ситуации. Так, например, можно выяснить, при каком условии санки въедут на асфальт на ¾ длины, что изменится, если начальная скорость санок будет другой и т.д. Варьируя формулировку условия задачи, можно значительно расширить спектр ее применения в учебном процессе.

Таким образом, поскольку при решении даже учебных физических задач не только создаются и оснащаются модели, но и проявляются их свойства, позволяющие прогнозировать процессы в широком диапазоне возможных условий, сами физические задачи можно считать универсальным и незаменимым средством обучения математическому моделированию.

Литература

1. Кондратьев А.С., Ляпцев А.В. Физика. Задачи на компьютере. – М.: Физматлит, 2008.

2. Тишкова С.А. Обучение учащихся обобщенному методу построения физической модели ситуации при изучении школьного курса физики: Дисс. … канд. пед. наук. – Астрахань, 2006. – С.13.

3. Ходанович А.И. Математическое моделирование на компьютере. Сборник задач и упражнений.– СПб.: Изд-во СПбГУКиТ, 2009.- 118 с.

4. методическое пособие для учителя. – СПб.: Изд-во ГРПУ им. А.И. Герцена, 2001

5. Бордовский Г.А., Кондратьев А.С., Чоудери А.Д.Р. Физические основы математического моделирования: Учеб. пособие для вузов – М.: Издательский центр «Академия», 2005. –320 с.

6. Клайн М. Математика. Поиск истины: Пер. с англ. – М.: Мир, 1988 – 295 с.

7. Ларченкова Л.А. Решение физических задач как средство диагностики и преодоления психолого-познавательных барьеров при обучении физике/ Физическое образование в вузах. Министерство образования и науки РФ.- М.: 2012.-Т. 18, №2.-– с.58-70

Рекомендовано  
Н.Ф.Радионова, доктор педагогических наук, член Редакционной Коллегии 

_____

Liudmila A. Larchenkova
Сandidate of Pedagogical Sciences, Associate Professor, Department of Theory and Methods of Teaching Physics, Al. Herzen State Pedagogical University of Russia, St. Petersburg
larludmila@yandex.ru 

Elena  V. Dolzhenko
Physics teacher, School № 369, St. Petersburg; Applicant for a Degree, Department of Theory and Methods of Teaching Physics, Al. Herzen State Pedagogical University of Russia, St. Petersburg
kvark0308@mail.ru  

Using the universality of mathematical models for teaching solving physics problems in high school

This article discusses the methodological possibilities of teaching some elements of mathematical modeling in solving physics problems in teaching physics in high school in terms of the universality of mathematical models.

Key words:
teaching solving physics problems, mathematical modeling of real phenomena, universality of mathematical models