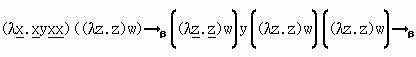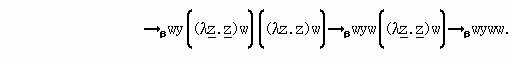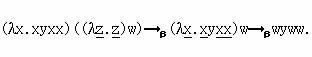Кудрявцева Ирина Андреевна
кандидат педагогических наук, доцент кафедры информационных систем и программного обеспечения; докторант кафедры информатизации образования Российский государственный педагогический университет им. А. И. Герцена, Санкт-Петербург.
Yarina22@gmail.com  

Интерпретатор λ-термов и его возможности в процессе обучения теоретическому программированию студентов IT-специальностей 

Аннотация
Представлен интерпретатор λ-термов и его возможности в процессе обучения теоретическому программированию. Данное средство поддерживает содержание обучения λ-исчислению, исчислению комбинаторов и фрагменту теории категорий (декартово замкнутой категории). Код интерпретатора написан на языке программирования Haskell, открыт для студентов и содержит библиотеки по работе с фундаментальными языковыми примитивами и операциями над ними. 

Ключевые слова:
теоретическое программирование, λ-исчисление, исчисление комбинаторов, декартово замкнутая категория, интерпретатор λ-термов, нормальный порядок β-редукции, аппликативный порядок β-редукции 

Предметом изучения теоретического программирования являются математические абстракции программ - предписаний, выраженных на специальных алгоритмических языках, обладающих определённой информационной  и логической структурой и подлежащих выполнению на компьютерах. Анализ теоретических исследований в области теоретического программирования показывает, что чаще всего используется математический аппарат, содержащий следующие взаимосвязанные разделы (по [1,с.27-28]): λ-исчисление, комбинаторная логика, теория типов языков программирования, теория категорий. 

Одним из разделов теоретического программирования является λ-исчисление, которое представляет собой:

1. метод построения функциональной абстракции, аппликации функций и исследования систем типизации;

2. средство для исследования проблем, возникающих в программировании (например, связанных с вызовами процедур, поскольку связанные переменные λ-исчисления соответствуют формальным параметрам процедур и функций);

3. средство для описания денотационной семантики языков программирования;

4. средство для разработки языков программирования (в частности, языков LISP,  ML, Haskell), закладывая в них определённые идеи математики. Например, использование λ-термов для определения функций, которые могут представлять собой данные; организация процесса вычисления в соответствии с основным правилом β-конверсии; возврат функции в качестве результата другой функции.

λ-исчисление, по своему внутреннему строению и наполнению, можно также трактовать как язык программирования, если:

1. примитивы для программирования выражать замкнутыми λ-термами, находящимися в нормальной форме;

2. базовые операции над примитивами также представлять замкнутыми λ-термами, находящимися в нормальной форме;

3. исполнение  программ сводить к последовательности β-преобразований.

Таким образом, наличие интерпретатора языка программирования чистого λ-исчисления позволит автоматизировать процесс преобразования одних λ-термов в другие, открывая возможность для исследования довольно широкого класса примитивов и базовых операций над ними как со стороны их представления в виде программ, так и с позиции эффективности их обработки (по количеству совершённых β-преобразований). 

Процесс погружения некоторого языка программирования в λ-исчисление в теоретическом программировании называется доказательством комбинаторной определимости базисных функций языка программирования. 

На данный момент нам известен лишь один интерпретатор бестипового λ-исчисления, написанный на языке программирования C – lci (автор K.Chatzikokolakis, 12.03.2006). 

Данный интерпретатор осуществляет вычислительный процесс в соответствии с нормальным порядком β-редукции. Для его использования в учебном процессе требуется знать встроенные в него функции и операторы, записанные во внутреннем представлении λ-термами. Эта информация извлекается из текстового файла, к которому интерпретатор обращается. Причём, данную базу функций можно пополнять или создавать собственный модуль функций. 

В итоге, весь процесс программирования сводится к тому, чтобы на "ассемблере" (с помощью λ-термов) выразить нужную функцию или оператор, а затем на языке "высокого уровня" (с помощью описанных функций и операторов) составлять выражения и композиции функций для запуска в интерпретаторе. На выходе результат вычисления оценивается количеством произведённых β-редукций и затраченным временем процессора. 

Для учебного процесса интерпретатор lci является хорошим подручным средством, однако в нём процесс распознавания термов и проведения нормального порядка β-редукции "спрятан" от обучаемых. 

Помимо этого  существует  интерпретатор λ-термов Lambda Animator (автор M.Thyer [2]), который лишь визуализирует разнообразные стратегии вычислений программ, записанных на языке Scheme. 

В связи с этим появилась идея создать интерпретатор λ-термов с открытым кодом на языке, доступном для быстрого понимания, и содержащим библиотеки по работе с фундаментальными языковыми примитивами и операциями над ними, расширив список λ-термов интерпретатора lci.

Для написания интерпретатора λ-термов чистого бестипового λ-исчисления был выбран функциональный язык программирования Haskell, поскольку в его основании находятся λ-исчисление (бестиповое и типизированное) и комбинаторная логика. 

В соответствии с индуктивным определением λ-терма была построена структура алгебраического типа данных "λ-терм" ("--" - комментарии):

Приведём примеры λ-термов на представленном выше языке:

Преобразования λ-термов осуществляются в соответствии с двумя стратегиями вычислений:

1. Нормальный порядок β-редукции.

Нормальным порядком β-редукции называется порядок проведения β-редукции, при котором вначале преобразовывается самый левый из самых внешних β-редексов. 

Понятие "самый левый из самых внешних редексов" определим индуктивным образом:

1. λ-терм (λx.s)t является своим самым левым из самых внешних редексов;

2. для λ-терма (st) самым левым из самых внешних редексов является самый левый из самых внешних редексов λ-терма s;

3. для λ-терма (λx.s) самым левым из самых внешних редексов является самый левый из самых внешних редексов λ-терма s.

Приведём пример нормального порядка β-редукции для λ-терма

На основе реализации операции "подстановка λ-терма N вместо всех свободных вхождений предметной переменной x в λ-терм M" и правила β-редукции смоделирована стратегия вычислений "нормальный порядок" [3,с.168-171]. Помимо этого в приведённом коде добавлена реализация α-конверсии и η-конверсии. 

2. Аппликативный порядок β-редукции.

Аппликативным порядком β-редукции называется порядок проведения β-редукции, при котором вначале преобразовывается самый левый из самых внутренних β-редексов. 

Понятие " самый левый из самых внутренних редексов" определим индуктивным образом:

1. λ-терм (λx.s)t является своим самым левым из самых внутренних редексов, если s не является редексом и t не является редексом;

2. для λ-терма (st) самым левым из самых внутренних редексов является самый левый из самых внутренних редексов λ-терма t, если t является редексом;

3. для λ-терма (st) самым левым из самых внутренних редексов является самый левый из самых внутренних редексов λ-терма s;

4. для λ-терма (λx.s) самым левым из самых внутренних редексов является самый левый из самых внутренних редексов λ-терма s.

Приведём пример аппликативного порядка β-редукции для λ-терма

Для организации и отображения процесса вычислений была написана функция по приведению λ-терма к нормальной форме: рекурсивное применение правила β-редукции к исходному λ-терму до тех пор, пока в результате никакой λ-подтерм не будет является β-редексом (т.е. следующий λ-подтерм примет вид предыдущего). В результате по полученному списку промежуточных термов видны изменения строения исходного терма. 

В заключение перечислим функциональные возможности интерпретатора λ-термов чистого бестипового λ-исчисления, отображённые в учебном пособии [3,с.460-487]. С помощью него возможно программирование:

1. Упорядоченных пар нумералов Чёрча, включая функции определения первого и второго элемента.

2. Логических констант, включая реализацию логических операций "И", "ИЛИ", "импликация", "логическое НЕ".

3. Элементов процесса вычислений, включая: (1) функцию для определения замыкания префиксным способом (let); (2) функцию для определения замыкания постфиксным способом (where); (3) функцию, моделирующую оператор ветвления; (4) функции, моделирующие комбинатор неподвижной точки для дальнейшей реализации рекурсивных функций: с вызовом по имени, с вызовом по значению (по Х.Карри); с вызовом по значению (по Д. Тромпу); с вызовом по значению (по А.Тьюрингу); (5) функцию, моделирующую примитивную рекурсию.

4. Элементов декартово замкнутой категории, содержащей следующие операции, часть которых описана выше: (1) тождество; (2) композиция (моделируется порядком расположения комбинаторов); (3) апплицирование (конструктор App); (4) декартово произведение (образование пары); (5) первая проекция (первый элемент пары); (6) вторая проекция (второй элемент пары); (7) спаривание функций; (8) каррирование; (9) декаррирование.

5. Нумералов Чёрча, включая: (1) различные варианты реализации арифметических функций над нумералами Чёрча (увеличение на единицу, сложение, умножение, возведение в степень, вычитание, уменьшение на единицу, преобразование пары нумералов в "следующую" пару нумералов, целочисленное деление нумералов с использованием комбинатора неподвижной точки); (2) предикаты над нумералами Чёрча (варианты реализации распознавания нумерала нуль, варианты реализации предиката "больше или равно"; "меньше или равно", "больше", "равно"); (3) модели кодирования натуральных чисел (преобразование десятичного натурального числа в нумерал Чёрча, преобразование нумерала Чёрча в десятичное натуральное число).

6. Одноуровневых  списков (нумералов, упорядоченных пар нумералов, символов), включая: (1) функции-конструкторы списков (создание пустого списка, добавление элемента в начало списка, конкатенация двух списков, выделение первого элемента списка - "головы", возвращение списка без первого элемента - "хвоста", создание списка из атома); (2) предикаты над списками (определение пустого списка); (3) транслятор структур (преобразование списка нумералов в список десятичных натуральных чисел; преобразование списка символов, записанного лямбда-термом, в список символов; преобразование списка пар, записанного лямбда-термом, в список пар десятичных натуральных чисел); (4) различные варианты конструирования списков с помощью функций-конструкторов списков; (5) модели функционалов.

7. Рекурсивных функций, включая: (1) различные варианты вычисления функций с использованием неподвижной точки (факториал нумерала, n-ое число Фибоначчи); (2) моделирование функций с помощью примитивной рекурсии (увеличение нумерала на 1, факториал нумерала); (3) моделирование функций Аккермана; (4) моделирование функций, возвращающих значение кусочно-заданной функции.

8. Комбинаторов, включая: (1) моделирование стандартных комбинаторов; (2) моделирование арифметических функций над нумералами с помощью комбинаторов (увеличение на 1; сложение, умножение, возведение в степень).

В результате нами построено средство обучения теоретическому программированию, поддерживающее содержание обучения λ-исчислению, исчислению комбинаторов и фрагменту теории категорий, относящемуся к декартово замкнутой категории.  

Литература

1. Вольфенгаген В.Э. Комбинаторная логика в программировании. Вычисления с объектами в примерах и задачах. М.: АО "Центр ЮрИнфоР", 2003. 336 с.

2. Thyer M. Lambda Animator. [Электронный ресурс] / - URL: http://thyer.name/lambda-animator/ - [дата обращения: 18.09.2014].

3. Кудрявцева И.А., Швецкий М.В. Элементы теоретического программирования: комбинаторная логика и теория типов. Часть I. СПб.: ЛЕМА, 2013. 488 с.

Рекомендовано к публикации:
А.В.Флегонтов, доктор физико-математических наук, член Редакционной Коллегии

______

Irina A. Kudryavtseva
Candidate of pedagogical sciences. Position: associate professor, department of information systems and software. Russian State Pedagogical University Herzen, St. Petersburg. The doctoral candidate of chair of informatization of formation of RGPU of A. I. Herzen, St. Petersburg.
Yarina22@gmail.com  

The interpreter of λ-terms in training to theoretical programming of students IT-specialties

The author presents an interpreter of λ-terms and its ability in learning theoretical programming. The tool support learning content λ-calculus, calculus combinators and a fragment of category theory (cartesian closed category). Code interpreter is written in Haskell, is open to students and contains a library for working with basic language primitives and operations on them. 

Keywords:
theoretical programming, λ-calculus, calculus combinators, cartesian closed categories, interpreter of lambda-terms, the normal order of β-reduction, applicative order of β-reduction 

Literatura

1. Volfengagen  V.Eh. Kombinatornaya logika v programmirovanii. Vychisleniya s obektami v primerakh i zadachakh. M.: AO "Centr YurInfoR", 2003. 336 s.

2. Thyer M. Lambda Animator. [Ehlektronnyj resurs] Ehlektron. dan. - Rezhim dostupa: http://thyer.name/lambda-animator/ (data obrashheniya: 18.09.2014).

3. Kudryavceva I.A., Shveckij  M.V. Ehlementy teoreticheskogo programmirovaniya: kombinatornaya logika i teoriya tipov. Chast I. SPb.: Lema, 2013. 488 s.