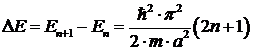Доронин Вячеслав Александрович
аспирант кафедры физической электроники, инженер кафедры физической электроники, Российский государственный педагогический университет им. А.И. Герцена, г. Санкт-Петербург
doroninslava@rambler.ru   

Остроумова Юлия Сергеевна
кандидат педагогических наук, заведующая кафедрой физики, Военная академия связи им. С.М. Будённого, г. Санкт-Петербург
sinklit@mail.ru  

Ханин Самуил Давидович
доктор физико-математических наук, заведующий кафедрой физической электроники Российский государственный педагогический университет им. А.И. Герцена, г. Санкт-Петербург
sinklit@mail.ru  

Освоение ключевых концептов нанофизики в исследовательском обучении при подготовке педагогических кадров

Аннотация
Обосновываются и раскрываются возможности освоения ключевых в нанофизике и наноэлектронике эффектов пространственного квантования энергии в рамках исследовательского обучения физике 

Ключевые слова
Пространственное квантование энергии, квантовые ямы, квантовые проволоки, квантовые точки 

Диктуемое запросами времени и обладающее значительным образовательным потенциалом освоение будущими учителями содержания проблематики физики наноструктур и наноэлектроники [1,2] требует своего научно-методического обеспечения и, прежде всего, определения характера обучения, адекватного его предмету. В настоящей работе обосновывается целесообразность и раскрываются возможности освоения ключевых концептов нанофизики в рамках исследовательского обучения – самостоятельного выполнения студентами соответствующих учебно-исследовательских заданий. В качестве ключевых концептов, необходимых для освоения, выступают размерные физические эффекты пространственного квантования энергии [3,4]. 

К основным достоинствам, определяющим целесообразность привлечения исследовательского обучения для достижения поставленной цели, относятся следующие:

• проблемная детерминация предметного содержания и процесса его развертывания в обучении;

• высокий уровень познавательной самостоятельности и активности обучающихся;

• сущностный (неформальный) характер приобретаемых знаний;

• возможность достижения содержательной и методологической целостности;

• востребованность принципиально важных для учителя видов деятельности;

• открытость образовательного содержания.

Для реализации этих достоинств предлагаемые студентам учебно-исследовательские задания должны отвечать, в своем содержании и организации выполнения, ряду требований, в том числе:

• личностно-смысловому значению изучаемой проблемы;

• включенности обучающихся в постановку проблемы, определение и реализацию методов её решения, критический анализ получаемых результатов;

• освоению необходимых знаний в логике задачного подхода;

• систематичности в представлении и решении определенной, обеспечивающей необходимую полноту приобретаемых знаний, последовательности (циклов) задач;

• взвешенное сочетание различных, адекватных содержанию задачи, форм её решения (аналитической, экспериментальной, численной), осуществляемых на соответствующих, координированных по тематике, видах занятий;

• синтеза приобретаемых обучающимися в результате решения задач новых для них знаний;

• логической завершенности в содержательном и методологическом аспектах каждого из заданий и учебно-исследовательской деятельности в целом;

• творческому участию самих обучающихся в расширении круга изучаемых вопросов и привлечении новых, необходимых для освоения, методов и средств решения задач.

Рассмотрим возможности построения учебно-исследовательских заданий, отвечающих указанным требованиям, на примере последовательности (цикла) заданий направленных на освоение квантовых размерных эффектов в системах пониженной размерности. Под последними понимают системы, в которых движение носителей заряда хотя бы в одном из измерений ограничено размерами, сравнимыми с дебройлевской длиной волны [3,4]. 

Начнем с определения особенностей электронного спектра в двумерных системах (квантовых ямах), где движение носителей заряда ограничено только в одном из направлений. Необходимый результат может быть получен в рамках решения хрестоматийной задачи квантовой физики об электроне в потенциальном ящике, приводящего к выводу о дискретном характере энергии электрона. Достаточно дополнить эту задачу следующим вопросом: определите ширину потенциального ящика, при которой расстояние между соседними энергетическими уровнями будет сравнимым со средней тепловой энергией при комнатной температуре.  

Используя известное, полученное при решении задачи в традиционной форме, выражение для расстояния между соседними энергетическими уровнями электронных состояний в потенциальном ящике

                      ,                                 

где -номер уровня,  – ширина потенциального ящика, обучающиеся приходят к выводу о том, что при уменьшении ширины потенциального ящика  до 100 нм энергетическое расстояние между соседними уровнями становится сравнимым с характерной тепловой энергией kT при комнатной температуре, так что имеет место пространственное квантование энергии, и описание электронных свойств двумерных наноразмерных систем следует производить с квантово-физических позиций. При этом, в отличие от трехмерных систем, энергетический спектр электронов в которых является квазинепрерывным и может быть изотропным, для двумерных систем имеет место анизотропный дискретно-непрерывный спектр с присущими ему подзонами размерного квантования:

                      ,                                     

где m^*-эффективная масса электрона. 

Полученный аналитический результат может быть экспериментально проверен в ходе лабораторного практикума. Здесь студентам предлагаются задания по сравнительному анализу спектральной зависимости коэффициента оптического поглощения при комнатной температуре в объемном (трехмерном) GaAs и двойной гетероструктуре (ДГС) инжекционного полупроводникового лазера, активной областью (узкозонным полупроводником, заключенным между двумя широкозонными) которой является квантовая яма того же состава и при низких температурах в ДГС с квантовыми ямами различной ширины. Обнаруживаемый синий сдвиг границы внутреннего фотоэффекта при уменьшении ширины ямы и количественное сопоставление опытных данных с расчетными, отвечающими вышеприведенной формуле для ΔE, подтверждают справедливость сделанных на основании аналитического решения задачи выводов. 

Далее, ставится аналогичный вопрос применительно к одномерным системам (квантовым нитям, проволокам): определите закон дисперсии для одномерных систем, в которых носители заряда могут свободно перемещаться только вдоль оси z (вдоль нити). 

В результате студенты приходят к выводу, что в одномерных системах пространственное квантование энергии происходит уже в двух направлениях x и y, так что закон дисперсии имеет вид:

                           ,                                      

где  и -целые числа, определяющие номер уровня энергии в направлении оси x и оси y соответственно. Подзоны размерного квантования при этом оказываются одномерными, нумеруемыми числами n₁ и n₂. 

Как и в предыдущем случае аналитическое решение задачи может быть дополнено экспериментальным, осуществляемым на соответствующих наногетерострукрурах.  

Задача, относящаяся к нульмерным системам (квантовым точкам, искусственным атомам), ставится сначала как экспериментальная в форме следующего задания практикума: определите спектральную зависимость коэффициента поглощения наночастиц полупроводника (например, сульфида свинца) различного размера, диспергированных в прозрачных диэлектрических матрицах (стеклах, полимерах, цеолитах).  

Опытным путем студенты определяют максимальную длину волны собственного поглощения полупроводника в зависимости от размера наночастиц, варьируемого от сотен до десятков ангстрем. Далее, для интерпретации полученных результатов, студентам предъявляется аналогичная предыдущим задача для аналитического решения: определите закон дисперсии для нульмерных систем, в которых движение носителей заряда ограничено во всех трех измерениях. 

Результат решения этой задачи – предельный случай пространственного квантования, когда энергетический спектр из дискретно-непрерывного, свойственного двумерным и одномерным системам пониженной размерности, становится исключительно дискретным, аналогичным энергетическому спектру атома:

                          ,                            

где - целое число определяющее номер энергетического уровня в направлении оси z. 

Изучение электронных свойств квантовых точек может быть продолжено в форме целостного по своему содержанию учебно-исследовательского задания, в котором прослеживается вся лежащая в основе изучения наноструктур цепочка “физика – материал – технология – применение”. Содержание занятия состоит в экспериментальном изучении фотолюминесценции матричных систем на основе стёкол с диспергированными в них квантовыми точками сульфида свинца, подвергнутых термообработке в различных режимах [5]. Последнюю студенты осуществляют самостоятельно и оценивают из спектров оптического поглощения средний размер квантовых точек в зависимости от условий формирования.  

Определяемый далее спектр фотолюминесценции имеющихся структур обнаруживает смещение его пика в длинноволновую область при увеличении размеров квантовых точек. Тем самым осваивается принцип управления длиной волны фотолюминесценции, имеющий важное значение в плане практического использования изучаемого материала в системах телекоммуникаций, а именно, в широкополосных волоконно-оптических усилителях [6,7]. 

Литература

1. Остроумова Ю.С. Подготовка студентов – будущих учителей – в области современных наукоемких технологий в контексте инновационного развития педагогического образования [Текст] / Ю.С. Остроумова // Вестник Северо-западного отделения Российской академии образования [Текст]. - 2013, - 1 (13). - С. 6-10.

2. Остроумова Ю.С. Обучение физическим основам современных наукоемких технологий при подготовке педагогических кадров: вопросы теории и практики: учебное пособие [Текст] / Ю.С. Остроумова. –СПб: Изд-во РГПУ им. А. И. Герцена, 2013. -123с.

3. Шик А.Я. Физика низкоразмерных систем: монография [Текст] / А.Я. Шик, Л.Г. Бакуева, С.Ф. Мусихин, С.А. Рыков. - Спб.: Наука, 2001. - 160с.

4. Нанотехнология: физика, процессы, диагностика, приборы [Текст] / под ред. В.В. Лучинина, Ю.М. Таирова. - М.: ФИЗМАТЛИТ, 2006.- 552 с.

5. Зимин С.П. Наноструктурированные халькогениды свинца: монография [Текст] / С.П. Зимин, Е.С. Горлачев. – Ярославль: ЯрГу, 2011. – 232с.

6. Liu C. Photoluminescence of PbS quantum dots embedded in glasses [Text] / C. Liu, J. Heo, X. Zhang, J.-L. Adam // J. Non-Cryst. Sol. – 2008. – Vol. 354. – P. 618–623.

7. Liu C. Absorption and photoluminescence of PbS QDs in glasses [Text] / C. Liu, Y.K. Kwon, J. Heo // J. Non-Cryst. Sol. – 2009. – Vol. 355. – P. 1880–1883.

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной коллегии

_____________

Vyacheslav A. Doronin
Post-graduate student of the Department of the physical electronics, engineer of the Department of the physical electronics, A.l. Herzen State Pedagogical University of Russia, St. Petersburg
doroninslava@rambler.ru 

Yulia S. Ostroumova
Candidate of Education Sciences, Head of the Department of the physics, S.M. Budyonny Military academy of telecommunications, St. Petersburg
sinklit@mail.ru  

Samuil D. Khanin
Doctor of Physics and Mathematics Sciences, Head of the Department of the physical electronics, A.l. Herzen State Pedagogical University of Russia, St. Petersburg
sinklit@mail.ru  

Development of the key concepts in nanophysics research training at the teacher training 

The development opportunities justified and disclosed the key effects spatial quantization of energy at the nanophysics and nanoelectronics in the framework of the research of teaching physics. 

Keywords:
Spatial quantization of energy, quantum wells, quantum wires, quantum dots 

Literatura

1. Ostroumova Yu.S.Podgotovka studentov – budushix ushiteley – v oblasti sovremennix naukoyomkix texnologiy v kontekste innovasionnogo razvitiya padagofisheskogo obrazovaniya [Text] / Yu.S. Ostroumova // Vestnik Severo-zapadnogo otdeleniya Rossiyskoy akademii obrazovaniya [Text]. – 2013, - 1(13). – S. 6-10.

2. Ostroumova Yu.S. Obusheniye fizisheskim osnovam sovremennix naukoyomkix texnologiy pri podgotovke pedagofisheskix kadrov: voprosi teorii I praktki [Text] / Yu.S. Ostroumova. – SPb.: Izd-vo RGPU im. A.I. Herzena, 2013. – 123s.

3. Chic A.Y. Fizika nizkorazmernish sistem: monografiya [Text] / A.Y. Chic, L.G. Bakueva, S.F. Musikhin, S.A. Rykov. – SPb: Nauka, 2001. – 160s.

4. Nanotexnologiya: fizika, prosessy, diagnostika, pribory [Text] / pod red. V.V. Lushinina, Yu.M. Tairova. – M.: FIZMATLIT,2006. – 552s.

5. Zimin S.P. Nanostrukturirovanniye shalikogenidy svinsa: monografiya [Text] / S.P. Zimin, E.S. Gorlachov. – Yaroslavl: YarGy, 2011. – 232s.

6. Liu C. Fotoluminiszensiya kvantovish tochek PbS vstroennish v stekla [Text] / C. Liu, J. Heo, X. Zhang, J.-L. Adam // J. Non-Cryst. Sol. – 2008. – Vol. 354. – P. 618–623.

7. Liu C. Poglosheniye i fotoluminiszensiya kvantovish tochek PbS v steklax [Text] / C. Liu, Y.K. Kwon, J. Heo // J. Non-Cryst. Sol. – 2009. – Vol. 355. – P. 1880–1883.