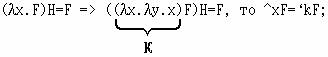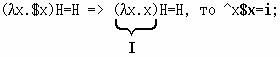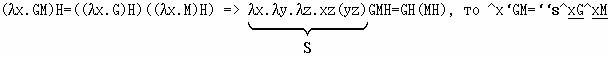Кудрявцева Ирина Андреевна
кандидат педагогических наук, доцент кафедры информационных систем и программного обеспечения; докторант кафедры информатизации образования, Российский государственный педагогический университет им. А. И. Герцена,  Санкт-Петербург
Yarina22@gmail.com  

Использование эзотерического языка Unlambda в процессе обучения теоретическому программированию студентов IT-специальностей 

Аннотация:
Автором выделены достоинства языка программирования Unlambda с позиции обучения теоретическому программированию. Рассмотрены основные сущности языка Unlambda, выражающие его функциональность и эзотеричность. В результате сформулированы положения, обосновывающие возможность использования языка Unlambda в процессе обучения теоретическому программированию. 

Ключевые слова:
теоретическое программирование, бестиповое λ-исчисление и исчисление комбинаторов, карринг (каррирование), исключение абстракции, комбинаторная характеристика комбинаторов S, K, I, равенство комбинаторов 

В данной статье обоснуем возможность включения языка программирования Unlambda в процесс обучения теоретическому программированию, которое связано с рассмотрением математических моделей программ, представляющих собой исчисления, рассматриваемые в математической логике, а именно: λ-исчисление и исчисление комбинаторов; часто в теоретическое программирование включают теорию типов и семантическую теорию языков программирования. Более того, метаязыком, используемым при описании математических моделей программ, является теория категорий. 

Язык Unlambda был изобретён Д.Мэдором [1] как эзотерический функциональный язык, основанный на комбинаторном исчислении в базисе {S,K} без использования операции абстракции (отсюда и название языка - Unlambda). Представим основные сущности языка Unlambda, которые выражают его функциональность и эзотеричность. 

1.  Ядро языка составляют следующие комбинаторы: (а) k (образования константы); (б) s (подстановки и композиции); (в) i (тождественный, i=skk). 

Отметим, что комбинаторы K и S, выраженные в языке соответствующими функциями k и s, представляют собой достаточный набор для того, чтобы сделать язык Unlambda замкнутым по Тьюрингу. Данный факт отражает мощь комбинаторного языка. 

Использование в  написании программ только двух комбинаторов делает язык Unlambda трудным и непонятным для непосвящённых, поэтому его относят к эзотерическим языкам программирования. Прилагательное в названии семейства языков происходит от гр. esoterikos - внутренний, тайный, скрытый, предназначенный для посвящённых [2]. 

2. Операция аппликации (`) применяет функцию к одному аргументу.

Для применения функции к нескольким аргументам требуется произвести каррирование этой функции. 

Каррингом (каррированием) (по [3,с.107]) называется явление, при котором для функции нескольких аргументов появляется возможность зафиксировать несколько первых из них: сам процесс фиксации аргументов и подготовка функции к возможности их фиксации. 

Каррированные функции "предполагают", что их можно применять к неполному числу аргументов (частичное применение), и результатом такого применения будут новые функции, которые "ожидают" на свой вход оставшиеся аргументы. 

Приведём пример применения операции аппликации для комбинаторов K и S. Вначале вспомним строение и комбинаторную характеристику базисных комбинаторов бестипового λ-исчисления: 

 

В языке Unlambda это записывается так: ``kxy=x; 

 

В языке Unlambda это записывается так: ```sxyz=``xz`yz. 

Операция аппликации в языке Unlambda способствует каррингу и придаёт ещё большую "функциональность" программам на этом языке. 

3. Примитивные функции.

Помимо функций, составляющих ядро языка Unlambda, существуют дополнительные функции [4], которые называются встроенными функциями (заметим, что отсутствуют функции, определяемые пользователем). 

Перечислим достоинства языка Unlambda с позиции его рассмотрения в обучении теоретическому программированию. 

1. Язык является математической моделью функционального стиля программирования на уровне комбинаторов, которая формирует представление о функциональном программировании на языке низкого уровня - языке комбинаторов в базисе {S,K,I}. Поэтому язык Unlambda можно рассматривать как язык ассемблера для машин "комбина'торной архитектуры", поддерживающих комбинаторный стиль программирования. 

Отметим, что существует высокоуровневый язык Haskell, на котором можно программировать с помощью встроенных комбинаторов K, I, B, C, а также известных комбинаторов λ-исчисления (например, S, W, Y), легко моделирующихся на данном языке. 

2. Умение конструировать программы на языке Unlambda можно трактовать как обязательный результат обучения  бестиповому λ-исчислению, в котором формируется представление о понятии "вычислимость".

Известно, что бестиповое λ-исчисление можно трактовать как язык программирования. Примитивами для программирования выступают замкнутые λ-термы, находящиеся в нормальной форме; базовые операции над примитивами также представляются замкнутыми λ-термами, находящимися в нормальной форме, а исполнение программ сводится к последовательности β-преобразований. Функциональные возможности интерпретатора λ-термов приведены в нашей статье [5]. 

Поскольку комбинатор - это замкнутый λ-терм, то для программирования на языке Unlambda достаточно иметь транслятор для перевода замкнутого λ-терма в комбинатор базиса {S,K,I}. Рассмотрим подробно процесс исключения абстракции (англ. unlambdaification) в языке Unlambda, опираясь на рекомендации, приведённые в статье [4]. 

Пусть λ - абстракция, обозначаемая далее по тексту в программной реализации символом "^", а $x - символ с переменным значением:

(1) если F - встроенная функция Unlambda, то ^xF является постоянной функцией со значением F; поскольку 

(2) если F=$x, то ^xF является значением $x; поскольку 

(3) если F=`GM, то ^xF является результатом применения аппликации G к M; поскольку 

 

Таким образом, процесс исключения абстракции можно автоматизировать. Просматривая выражение F с абстракцией (^x) слева направо и встречая: (1) символ '`' - заменяем его на ``s; (2) переменную $x (совпадающую по названию с переменной абстракции) - заменяем её на i; (3) встроенную или любую другую переменную, отличную от $x, - приписываем к ней префикс `k. 

Приведём пример преобразования нумерала Чёрча, выраженного замкнутым λ-термом, в комбинатор базиса {S,K,I}:

 

Теперь продемонстрируем результаты трансформации λ-термов в комбинаторы языка Unlambda для моделирования элементов потока управления, а также арифметических функций над нумералами Чёрча:

(а) построим функцию для вывода нумерала n в виде последовательности n символов '*' по λ-терму, представляющему собой композицию встроенных функций Unlambda [4]: 

 

(б) построим функцию для умножения двух нумералов на языке λ-термов: 

 

Доказательство утверждения ‘’s’’s’ksk’ki=i 

 

В результате последовательности трансформаций программа на языке Unlambda будет выглядеть так (# - однострочный комментарий): 

 

При запуске программы на экран будут выведены два символа '*';

(в) построим функцию организации ветвления алгоритма на языке λ-термов: 

 

В результате последовательности трансформаций программа на языке Unlambda будет выглядеть так: 

 

При запуске программы на экран выведется символ '*' (нумерал 1). Если в программе поменять значение "Истина" на значение "Ложь" 

 

то на экран будут выведены два символа '*' (нумерал 2). 

В заключение упомянем организацию циклических процессов. Известно, что в теории бестипового λ-исчисления существуют комбинаторы неподвижной точки для организации процесса рекурсии. Поэтому, имея реализацию рекурсивной функции на языке λ-термов, можно с помощью транслятора получить программу на языке Unlambda. 

3. Автоматический вывод программ на языке Unlambda из соответствующих λ-термов, а также знание строения некоторых комбинаторов позволит пополнять набор равенств комбинаторов и впоследствии упрощать программы на языке Unlambda. 

Например, приведённые выше выкладки по преобразованию нумерала one в комбинатор базиса {S,K,I} привели к результату, отличному от результата, приведённого в [4]. Итак, появляется утверждение 

 

которое требует доказательства: 

 

Теперь доказанным утверждением можно пополнить базу равенств комбинаторов в программе по упрощению программ на Unlambda. 

Подводя итоги, отметим, что язык Unlambda:

(1) является концептуальным низкоуровневым языком теоретического программирования;

(2) является (как эзотерический язык) хорошей проверкой знаний элементов  бестипового λ-исчисления: программирование в терминах λ-термов и построение доказательств λ-формул;

(3) представляет собой реальный язык программирования при наличии набора комбинаторов, полученных из примитивов и операций бестипового λ-исчисления;

(4) имеет множество реализаций на разных языках программирования (CAML, Java, Perl, Scheme, SML) [4], одна из которых представлена на языке C (D.A.Madore,1999). 

Кроме этого, нами [6,с.418-422] написан транслятор на языке Haskell по преобразованию λ-термов в комбинаторы базиса {S,K,I} и упрощению полученных комбинаторов в соответствии с базой равенств комбинаторов. 

Литература

1. Unlambda. [Электронный ресурс] - URL: http://ru.wikipedia.org/wiki/Unlambda  [дата обращения: 06.01.2015]

2. Комлев Н.Г. Словарь иностранных слов. М.: Эксмо, 2006. 672 с.

3. Кирпичёв Е.Р. Элементы функциональных языков // Практика функционального программирования, 2009, 3, с.83-197.

4. Madore D. The Unlambda Programming Language. [Электронный ресурс] - URL: http://www.madore.org/~david/programs/unlambda/  [дата обращения: 08.01.2015].

5. Кудрявцева И.А. 10 функциональных возможностей интерпретатора λ-термов в обучении теоретическому программированию // Информационные системы и технологии. Межвузовский сборник научно-технических статей. №3. СПб.: РГПУ им. А.И.Герцена, 2014, с.59-63.

6. Кудрявцева И.А., Швецкий М.В. Элементы теоретического программирования: комбинаторная логика и теория типов. Часть I. СПб.: ЛЕМА, 2013. 488 с.

Рекомендовано к публикации:
А.В.Флегонтов, доктор физико-математических  наук, член Редакционной Коллегии

               

Irina A. Kudryavtseva
Candidate of pedagogical sciences, Associate professor, Department of information systems and software; Doctoral candidate of Department of informatization of education, Al.Herzen State Pedagogical University of Russia, St. Petersburg
Yarina22@gmail.com  

Use Unlambda esoteric language in the learning process of theoretical programming students IT-specialties 

The author allocates advantages of programming language Unlambda with positions of training to theoretical programming. The basic are considered essence of language Unlambda, expressing its functionality and esoteric. As a result, stated justifications for the use of language in the learning process Unlambda theoretical programming. 

Key words
theoretical programming,  untyped  lambda  calculus, combinators calculus, currying, abstraction exception, combinatorial characteristic of the combinators S, K, I, equality of combinators 

Literature

1. Unlambda. [Ehlektronnyj resurs]  - URL: http://ru.wikipedia.org/wiki/Unlambda  [data obrashheniya: 06.01.2015].

2. Komlev N.G. Slovar inostrannykh slov. M.: Ehksmo, 2006. 672 s.

3. Kirpichjov E.R. Ehlementy funkcionalnykh yazykov // Praktika funkcionalnogo programmirovaniya, 2009, 3, s.83-197.

4. Madore D. The Unlambda Programming Language. [Ehlektronnyj resurs]  - URL: http://www.madore.org/~david/programs/unlambda/  [data obrashheniya: 08.01.2015].

5. Kudryavceva I.A. 10 funkcionalnykh vozmozhnostej interpretatora λ-termov v obuchenii teoreticheskomu programmirovaniyu // Informacionnye sistemy i tekhnologii. Mezhvuzovskij sbornik nauchno-tekhnicheskikh statej. №3. SPb.: RGPU im. A.I.Gercena, 2014, s.59-63.

6. Kudryavceva I.A., Shveckij M.V. Ehlementy teoreticheskogo programmirovaniya: kombinatornaya logika i teoriya tipov. Chast I. SPb.: LEMA, 2013. 488 s.