| ||||||||||||||||||||||||
|
The Emissia.Offline Letters Электронное научное издание (научно-педагогический интернет-журнал) | ||||||||||||||||||||||||
|
Издается с 7 ноября 1995 г. Учредитель: Российский государственный педагогический университет им. А.И.Герцена. ISSN 1997-8588 | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Сосновский Юрий
Михайлович
Хмырова Наталья
Анатольевнакандидат физико-математических наук, доцент кафедры «Физика и
химия»,
Омский государственный университет путей сообщения, г. Омск. Решение контекстных задач по физике как метод оценки компетентностей студентов технических университетов
Аннотация
Ключевые слова Каждому преподавателю ВУЗа известно, как трудно научить чему-либо студентов, если они не проявляют интереса к содержанию данного предмета. Это особенно заметно при преподавании не специализированных предметов студентам I-II курсов. Ситуация усугубляется подборкой, зачастую, весьма абстрактных задач для решения на практических занятиях. Между тем, компетентностный подход к содержанию образования предполагает развитие способности использовать теоретические знания для решения профессиональных задач [1]. Иными словами, по нашему мнению, реализация компетентностного подхода требует использования контекстных физических задач, вариация которых по сложности позволяет разработать методику оценки профессиональной компетентности студентов в техническом университете. По мнению А. А. Вербицкого, компетентность это реализованная на практике компетенция [2]. Контекстным является такое обучение, в котором на языке наук и с помощью всей системы форм, методов и средств обучения (традиционных и новых) последовательно моделируется предметное и социальное содержание будущей профессиональной деятельности студентов [3]. Умение решать контекстные задачи первого, второго и третьего (самого сложного) уровней, можно интерпретировать как проявление компетентности первого (начального, репродуктивного), второго (среднего, поискового) и третьего (высшего, творческого) уровня. Контекстная задача – это в известном смысле - мотивационная задача, в условии которой описана конкретная жизненная ситуация (в нашем случае - профессиональная). Алгоритм решения таких задач включает:
Несмотря на то, что в физике большую часть задач можно отнести к контекстным задачам, в высшем техническом учебном заведении особую роль должна играть профессиональная направленность этих задач. Кроме того, задача должна обеспечивать усвоение форм и процедур задачной деятельности, а также отвечать стандартам научности в области математики [4]. И. Я. Лернер выделял три фактора сложности учебно-познавательной задачи [5]:
Контекстная задача выступает и как способ актуализации личностного потенциала студента, пробуждения смысла поисковой активности, осознание ценности изучаемого материала [6]. Практика показывает, что разработка контекстных заданий, способствующих оценке этого качества, базируется на определённых принципах:
Рассмотрим пример контекстной задачи трех разных уровней сложности, Задача разработана (в продолжение предыдущих работ [8, 9]) для практического занятия по физике (раздел «Механика») со студентами первого курса Омского государственного университета путей сообщения, обучающихся по специальностям 190300 «Подвижной состав железных дорог» и 190901 «Системы обеспечения движения поездов». Задача: Железнодорожный состав подходит к станции имея скорость 50 км/час. Рассчитайте путь и время до полной остановки состава. Первый уровень сложности: Считать движение прямолинейным и равнозамедленным. Модуль ускорения равен 0,3 м/c2. Решение данной задачи основано на применении основных формул школьной кинематики.
Для прямолинейного движения пройденный путь поезда до остановки
равен модулю вектора перемещения. Его находим исходя из формулы:
Время до полной остановки можно найти из формулы
Тогда, с учётом проекции:
Второй уровень сложности: Первые 15 секунд состав двигался равнозамедленно с ускорением 0,3 м/с2, затем 20 секунд с ускорением 0,1 м/с2 и оставшиеся 15 секунд опять равнозамедленно с ускорением 0,2 м/с2. Найдите путь пройденный составом до полной остановки. Условие этой задачи более реально, т.к. в действительности состав не может все время двигаться с постоянным ускорением. Для решения данной задачи полезно построить графики скорости и ускорения.
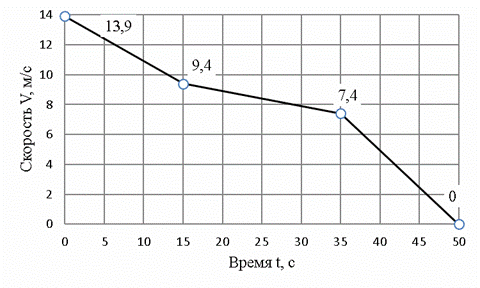
Для построения зависимости скорости состава от времени, необходимо
знать значения скорости в момент времени 15 и 35 секунд. Используя
формулу
Рис. 1 Зависимость скорости состава от времени. Дальнейшее решение имеет несколько вариантов, одно из которых заключается в нахождении площади под графиком скорости. Тогда
Произведём вычисления:
Третий уровень сложности: Скорость состава меняется согласно таблице:
Определить путь пройденный составом до полной остановки за это время. Решение задачи в такой постановке, как правило, вызывает у студентов большие трудности. Во-первых, такое движение (нелинейный характер зависимости скорости состава от времени виден из табличных данных) нельзя описать формулами для равноускоренного движения.
Во-вторых, решение такой задачи без использования компьютера займёт
достаточно большое количество времени (основное время потребуется
для нахождения аппроксимационной зависимости
В-третьих, студент должен обладать определёнными навыками работы с математическими пакетами.
Основная идея в решении задачи может быть выражена одной формулой:
График зависимости скорости состава от времени показан на рис.2. Однако, стандартные действия, основанные на нахождении формульной зависимости скорости от времени на всём временном отрезке приводят к очень приближённым выражениям имеющим достаточно низкий коэффициент корреляции.
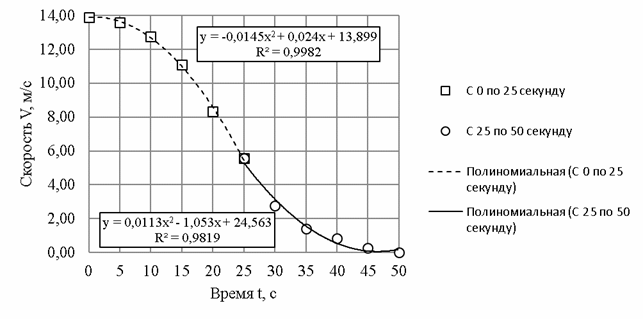
Рис.2 Зависимость скорости состава от времени с полиномиальными аппроксимациями второй степени на двух временных отрезках. Выход из подобной ситуации может состоять в разбиении всего временного интервала на два участка и нахождении формульной зависимости по отдельности.
Для временного интервала от 0 до 25 секунды зависимость скорости
состава от времени (с учётом перевода скорости в размерность СИ)
описывается уравнением:
Следует заметить, что
величина достоверности аппроксимации для первой и второй зависимости
достаточно высока:
Дальнейшее решение сводится к нахождению суммы двух определённых интегралов:
В результате имеем:
Полученный результат согласуется с ранее полученными результатами, рассмотренными в предыдущих примерах. Применение контекстных задач, ориентированных на актуализацию личностного потенциала, пробуждения смысла поисковой активности, осознание ценности изучаемого материала и на будущую профессию студентов, может способствовать:
Следует обратить особое внимание на комплексный характер содержания и способов решения таких задач. Для решения задач такого типа, студент должен не только хорошо знать основные законы физики, но и хорошо владеть математическим аппаратом (на уровне дифференцирования и интегрирования) и уверенно пользоваться основными компьютерными программами. Все эти смысловые компоненты могут являться критериями оценки компетентности будущих инженеров. Внедрение подобных задач в практику подготовки специалистов с высшим профессиональным техническим образованием соответствует современным требованиям к оценке деятельности студентов и открывает перспективы дальнейших исследований. Литература
Рекомендовано к
публикации:
Yruiy
M. Sosnovsky
Natalya А.
Khmyrova
Solution of contextual tasks in physics as method of an assessment of kompetentnost of students of technical universities Developed contextual problems in physics with a professional orientation with three difficulty levels, the use of which in the learning process enables the teacher to assess students' competence.
Keywords Literature
| ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
| Copyright (C) 2015, Письма в
Эмиссия.Оффлайн (The Emissia.Offline Letters) ISSN 1997-8588. Свидетельство о регистрации СМИ Эл № ФС77-33379 (000863) от 02.10.2008 от Федеральной службы по надзору в сфере связи и массовых коммуникаций При перепечатке и цитировании просим ссылаться на " Письма в Эмиссия.Оффлайн ". Эл.почта: emissia@mail.ru Internet: http://www.emissia.org/ Тел.: +7-812-9817711, +7-904-3301873 Адрес редакции: 191186, Санкт-Петербург, наб. р. Мойки, 48, РГПУ им. А.И.Герцена, корп.11, к.24а |
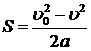 .
.
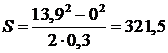
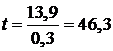
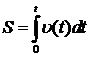 .
.
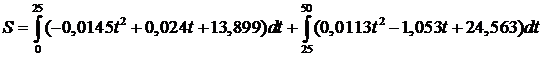 .
.