Калинова Юлия Александровна,
педагог дополнительного образования, лицей № 393, С-Петербург
juliakalinova@bk.ru

Развитие дивергентного мышления при изучении геометрии в 7- 9 классах

Аннотация
В статье рассмотрены дивергентные задачи по планиметрии как средство развития дивергентного мышления учащихся и методика работы с ними (приемы активизации, привлечение субъектного опыта учащихся при работе с задачей).

Ключевые слова 
креативность, дивергентное мышление, дивергентная задача по планиметрии, субъектный опыт

Одним из важнейших качеств, позволяющих человеку приспособиться к жизни, является креативность – способность создавать новое, порождать необычные идеи, отклоняться в мышлении от традиционных схем. Психологи начала XX в. не выделяли креативность как особую способность, отождествляли ее с интеллектом. Ситуация изменилась в 60-х гг. XX века. К этому времени был накоплен масштабный опыт тестирования интеллекта, поставивший перед исследователями ряд вопросов. В частности, выяснилось, что профессиональные и жизненные успехи вовсе не напрямую связаны с уровнем интеллекта, вычисляемым с помощью тестов IQ. Опыт свидетельствовал, что люди с не очень высоким IQ оказываются способны на незаурядные достижения, а многие другие, чей IQ значительно выше, нередко от них отстают. Было высказано предположение, что здесь решающую роль играют какие-то иные качества ума, которые не охвачены традиционным тестированием. Такую способность назвали креативностью [1]. 

Одним из первых исследователей креативности был Дж. Гилфорд. Он ввел в научный обиход понятие «дивергентное мышление» [2]. Дж. Гилфорд указал на принципиальное различие между двумя мыслительными операциями: конвергенцией и дивергенцией. Конвергентное мышление актуализируется в том случае, когда человеку, решающему задачу, надо на основе множества условий найти единственно верное решение. Дж. Гилфорд отождествил способность к конвергентному мышлению с тестовым интеллектом, то есть интеллектом, измеряемым высокоскоростными тестами IQ. Дивергентное мышление определяется Дж. Гилфордом как «тип мышления, идущий в различных направлениях». Такое расходящееся мышление позволяет менять направление поиска в процессе нахождения ответов на различные вопросы, что ведет к появлению целого веера разнообразных и неожиданных решений и результатов. Оно связано с уходом от привычного и ожидаемого, даже от логики, допускает внезапные ассоциативные переходы. Дивергентное мышление – мышление целостное, интуитивное, альтернативное, опирающееся на воображение, позволяющее порождать много разнообразных оригинальных идей на основе однозначных данных в нерегламентированных условиях деятельности. 

Для измерения креативности Дж. Гилфорд ввел понятие дивергентной задачи, или задачи с открытым концом – то есть задачи, имеющей неограниченное количество решений. Он противопоставлял их задачам с закрытым концом, используемым в традиционных тестах интеллекта и имеющих единственно верный ответ.

Пример тестового задания с закрытым концом.  «Лом – мол;    куб – бук;    сон – …».  Какое слово нужно поставить вместо многоточия?

Пример тестового задания с открытым концом.  Напишите предложения из четырех слов, в котором каждое слово начинается с указанной буквы. «Б…у…ж…б…».

Первый тест имеет однозначный ответ: нос. Второй тест не имеет однозначного ответа. Можно придумать много различных ответов. Приведем примеры. Бесполезно убивать желтых букашек. Билеты унесла жена булочника  и т.д. В ходе исследований было установлено, что одним людям легче выполнять тесты первого типа,  другим – второго. По мнению Дж. Гилфорда при выполнении этих двух тестов происходят принципиально различные мыслительные процессы: в первом случае человек мыслит в одном направлении, а  во втором – в разных. В соответствии с теорией  Дж. Гилфорда у людей, которые лучше справляются с тестами первого типа, преобладает однонаправленное (конвергентное) мышление, а у людей, которым легче даются тесты второго типа, – разнонаправленное (дивергентное) мышление. Именно второй тип мышления лежит в основе творчества.  

Различными авторами разрабатывались программы по развитию дивергентного мышления. В большинстве этих программ используются задания и вопросы дивергентного типа, т.е. задания, допускающие множество приемлемых ответов. Ученики получают эти ответы, работая с картинками, игрушками и даже звуками, которые они воспринимают, прослушивая магнитофонную запись [3]. Следует отметить, что большинство программ по развитию дивергентного мышления совершенно не связаны с содержанием школьной программы. Не существует разработок, позволяющих развивать дивергентное мышление учащихся основной и старшей школы на уроках математики. Поэтому необходимо создание учебных курсов, в которых развитие дивергентного мышления осуществляется на материале школьной программы, в частности, по математике. Мы разработали задания с открытым концом (предполагающие множество приемлемых ответов) на материале планиметрии.  Как показывает опыт, для успешного решения задач с открытым концом требуется большая мотивация, чем для решения задач с закрытым концом. Иначе придуманные учащимися варианты будут банальными. Поэтому при работе с такими задачами учителю необходимо использовать приемы активизации учащихся. Нами были выделены три приема активизации. Рассмотрим каждый из них.

Первый прием активизации. Постановка развивающей цели занятия.

Учитель может объяснить детям, что решая подобные задачи, они развивают в себе дивергентное мышление и предложить выполнить тестовые задания на дивергентное мышление, например, такое.  Обычное употребление газеты: ее читают. Найдите 20 других способов употребления газеты. И только уже после этого предлагать математические задачи с открытым концом.

Второй прием активизации. Привлечение субъектного опыта учащихся.

При работе с задачами с открытым концом целесообразна работа, связанная с выявлением и дальнейшим обогащением субъектного опыта учащихся. Рассмотрим это на следующем примере. Одним из видов задач  с открытым концом являются задачи на придумывание определений геометрических понятий. Для того чтобы актуализировать субъектный опыт учащихся подобные задачи можно предлагать в следующей форме.

Задание. Представьте себе, что вы разговариваете по телефону со своим другом, и вам нужно объяснить, что такое квадрат. Вы можете употреблять любые слова, кроме самого слова «квадрат». Попробуйте это сделать разными способами.

Приведем примеры ответов, придуманных учащимися в ходе нашего эксперимента.

• Клетка в тетради по математике.

• Слово, состоящее из семи букв, первая из которых «к», вторая –  «а», …, последняя – «т».

• Круг с четырьмя углами.

• Название черной фигуры Малевича.

В процессе данной работы учащиеся очень редко обращались к геометрическим терминам. Самым распространенным из логически правильных определений связанных с геометрией было следующее: квадрат – это прямоугольник с равными сторонами. После этого мы предложили учащимся выполнить ряд упражнений, которые должны подсказать им другие способы выполнения задания. Приведем примеры ответов, придуманных учащимися после выполнения всех упражнений.

• Прямоугольник, у которого диагонали взаимно перпендикулярны.

• Ромб, около которого можно описать окружность.

• Геометрическая фигура, являющаяся одновременно прямоугольником и ромбом.

• Параллелограмм, имеющий ровно четыре оси симметрии.

• Объединение двух равнобедренных прямоугольных треугольников с общей гипотенузой.

• Правильный четырехугольник.

• Грань куба.

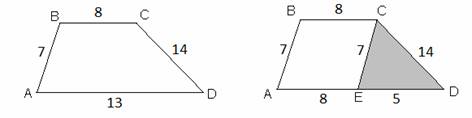
Третий прием активизации. Применение игровой деятельности.

Среди приемов активизации также следует выделить активное взаимодействие между участниками учебного процесса, включение игровых моментов с элементами соревнования. Рассмотрим это на примере следующей задачи с открытым концом.

Задание.  Придумайте несколько несуществующих геометрических фигур.

В качестве примера несуществующей фигуры приведем один из вариантов, придуманных учащимися: трапеция с основаниями 8 и 13 и боковыми сторонами 7 и 14 (рис. 1). Эта фигура не существует, поскольку если провести СЕ параллельно АВ, то в треугольнике CDE стороны будут равны 5, 7, 14. Но стороны такого треугольника не удовлетворяют неравенству треугольника, значит, он не существует, значит и описанной фигуры не существует. 

рис. 1. Иллюстрация к заданию: придумать несуществующую геометрическую фигуру

Для того чтобы создать у учащихся установку на придумывание фигур, несуществование которых неочевидно, можно использовать следующий прием: предложить учащимся придумывать фигуры с тем чтобы потом задать другому человеку вопрос: «Существует данная фигура или нет?». Данной работой по придумыванию фигур учащиеся могут заниматься и в школе,  и дома. Но в любом случае необходимо чтобы каждую придуманную задачу учащийся мог с кем-нибудь обсудить. Можно организовать работу так, чтобы этим  другим человеком оказался сосед по парте, другие ученики класса, даже сам учитель.  

Можно организовать соревнование между учащимися, для этого класс необходимо разделить на две команды. Игра проводится в несколько этапов. На первом этапе каждая команда придумывает определенное количество фигур, часть из которых существует, часть нет  (их может быть, например, шесть) и оформляет их описания на листке. На втором этапе команды обмениваются этими листками и пытаются определить по поводу каждой из фигур, придуманных соперниками, существует она или нет. На третьем этапе проводится собственно игра, в процессе которой обсуждается каждая из придуманных фигур. Допустим, некоторую фигуру придумала команда № 1, а определяла, существует ли она, команда № 2. В процессе игры эту фигуру обсуждают ответчик из команды  № 2 и оппонент из команды № 1. Сначала выступает ответчик. Он должен высказать свое мнение по поводу того, существует фигура или нет, и привести доказательство этого. После этого выступает оппонент. Он должен сообщить, какие он нашел ошибки и недочеты в решении ответчика. Важно чтобы команда, придумавшая фигуру, сама знала ответ на вопрос, существует эта фигура или нет. Поэтому при необходимости ответчик и оппонент меняются ролями, и тогда выступающий из той команды, которая придумала фигуру, должен объяснить, почему фигура существует или не существует. После обсуждения очередной фигуры командам начисляются баллы. 

Таким образом, работу по развитию дивергентного мышления можно проводить при овладении учащимися школьной программы, что сделает обучение в школе более  творческим.

Литература

1. Пономарёв,  Я.А. Психология творчества. – М.: Наука, 1976.

2. Гилфорд, Дж. Три стороны интеллекта // Психология мышления - М.: Прогресс, 1965.

3. Иванов, А. Н. Задачи конвергентные и дивергентные / А. Н. Иванов // Начальная школа: до и после. № 7. 2007.

Рекомендовано к публикации:
Н.С. Подходова, доктор педагогических наук, научный руководитель работы
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

________

Julija A. Kalinova
teacher of complementary education, school №  393, S-Peterburg.
juliakalinova@bk.ru

The development of divergent thinking in studying geometry in 7- 9 classes

In the article the divergent problems of Planar geometry as a means of development of divergent thinking of students and how to work with them (the techniques of revitalization, attracting regional experience students to work with the task).

Key words: creativity, divergent thinking, divergentnaâ task of Planar geometry, based on the subjective experience

1. Ponomarev Ja. A. Psihologija tvorchestva. – M.: Nauka, 1976.

2. Gilford Dg. Tri storoni intellekta // Psihologija mislenija – M.: Progress, 1965.

3. Ivanov A.N. Zadachi convergentnie i divergentnie/  A.N. Ivanov // Nachalnaja scola: do i posle. № 7. 2007.