Болух Ольга Валерьевна
аспирант кафедры методики обучения математике и информатике, Российский государственный педагогический университет им. А. И. Герцена,  Санкт-Петербург
bolukholga@mail.ru  

Снегурова Виктория Игоревна
доктор педагогических наук, профессор, заведующая кафедрой методики обучения математике и информатике, Российский государственный педагогический университет им. А. И. Герцена,  Санкт-Петербург
kafedra.mom@gmail.com  

Требования к системе задач, способствующей формированию действия «прогнозирования»

Аннотация:
Описана система задач, направленная на формирование действия «прогнозирования» в процессе обучения геометрии в основной школе. Сформулированы требования к содержанию данной системы задач.

Ключевые слова:
система задач по геометрии, требования к системе задач, конструирование системы задач

Цель настоящей работы  состояла в  конструировании системы задач, направленной на формирование действия «прогнозирования» в процессе обучения геометрии в основной школе,  и формулировании требования к ее содержанию. В известной нам литературе данный вопрос ранее не затрагивался.

Благодаря исследованиям Г.А. Балла [1], П.Я. Гальперина [2], В.В. Давыдова [4], Е.И. Машбица [7] и ряда других  теория учебных задач является сегодня хорошо разработанной ветвью научного знания.  Проблемам конструирования учебных задач (систем учебных задач) по математике посвящены исследования  Е.А. Демидовича [5] и А.А. Максютина [6]. Однако, работ по проектированию системы учебных задач по геометрии в основной школе, способствующей формированию действия «прогнозирования» нам неизвестно.

Вместе с тем, имеется насущная необходимость в конструировании  «универсальной» системы задач как множества упорядоченных задач, связанных между собой и направленных на формирование действия «прогнозирования» на уроках геометрии в основной школе. Здесь под термином  «задача»  понимается такая задачА, при решении которой в ученике происходят заранее заданные изменения, и он овладевает общим способом решения большого круга "частных задач" (вслед за В. В. Давыдовым [3]). Конструируя систему,  сформулируем требования к ее содержанию. Будем считать сформированным действие «прогнозирование», если  учащийся:

- владеет всеми умениями, входящими в состав действия «прогнозирование», в том числе умениями:

• воспринимать и извлекать информацию;

• сравнивать полученную информацию с имеющимися знаниями;

• ставить цель и формулировать задачу; составлять план и последовательность действий;

• обобщать, моделировать и организовывать информацию, полученную из условия задачи в виде чертежа, краткой записи;

• обнаружить отклонения и отличия от эталона;

• сличать способ действия и его результат с заданным эталоном;

• корректировать решение задачи, вносить необходимые дополнения и коррективы в план и способ действия.

- может свободно использовать эти умения по отдельности и группы умений  при решении математической задачи без прямого указания на необходимость его применения.

Для обеспечения условий формирования действия «прогнозирования», нужно прежде всего создать условия для обучения учащихся каждому умению, входящему в действие «прогнозирование». Этого можно добиться, предлагая учащимся задачи, решение которых способствовало бы формированию каждого умения в отдельности и  группы умений.

Таким образом, первое требование к содержанию системы задач состоит в том, что  в системе нужны задачи, решение которых способствует формированию и отработке одного из умений, входящих в состав действия «прогнозирования». Такие задачи будем называть задачами первого уровня –  «простейшими задачами». Приведем типичный пример такой задачи:
Какую бы задачу ты сформулировал для своего соседа по парте? Решение этой задачи основано на применении умения ставить цель и формулировать задачу.

Второе требование формулируется следующим образом: в системе нужны задачи, при решении которых формируется группа умений, входящая в состав действия «прогнозирования» таких, как аналитическая, диагностическая, прогностическая, коррекционная. Такие задачи будем называть задачами второго уровня - «задачи для  группы умений».  К таким задачам относятся:

- задачи, направленные на формирование группы аналитических умений. Задачи, представленные в данной группе, формируют умения воспринимать и извлекать информацию, анализировать и сравнивать информацию, т.е. все эти умения в совокупности.

- задачи, направленные на формирование группы диагностических умений. Задачи, представленные в данной группе, направлены на формирование умений ставить задачу и цель, представить информацию в определенном порядке или по определенной схеме, составлять план и последовательность действий, т.е. все эти умения в совокупности.

- задачи, направленные на формирование группы прогностических умений. Задачи, представленные в данной группе, формируют умения обобщать информацию, моделировать и организовывать информацию, полученную из условия задачи, в виде чертежа и краткой записи, т.е. все эти умения в совокупности.

- задачи, направленные на формирование группы коррекционных умений. Задачи, представленные в данной группе, формируют умения оценивать результат деятельности, анализировать полученный опыт, контролировать ситуацию, корректировать информацию, т.е. все эти умения в совокупности.

Но формирования отдельных групп умений недостаточно для формирования действия «прогнозирования». Нужны задачи, решение которых опирается в равной мере на использование нескольких групп умений в совокупности. Это представляет собой третье требование к содержанию системы задач. Такие задачи будем называть задачами третьего уровня - «интегрированные задачи». К ним относятся задачи, при решении которых мы будем формировать все группы умений в совокупности.

Для того чтобы предоставить возможность формировать действие «прогнозирование» каждому учащемуся, в системе нужны задачи разного уровня сложности. Таким образом, четвертое требование можно сформулировать так: система должна содержать задачи разного уровня сложности.

По определению А.А.Столяра сложность - это объективная характеристика, заключающаяся в количестве составляющих подзадач    [8]. Задачи первого уровня сложности (минимальный) - это в основном задачи на воспроизведение известных формул или способов решения, практически не требующие обоснований при их решении. Они будут характеризоваться очевидностью способа решения или доказательства, небольшим (не больше трех) количеством шагов решения или доказательства.

При переходе ко второму уровню сложности (средний) усложняется математический материал, входящий в условие, способ решения не совсем очевиден и требует небольшого количества обоснований, увеличивается количество действий, которое нужно выполнить для решения или доказательства.

Задачи третьего уровня сложности (повышенный) характеризуются не столько технической сложностью, сколько неочевидностью возможного способа решения, они предполагают наличие нескольких способов решения, каждый из которых требует своей последовательности обоснований.

Пятое требование формулируется таким образом:  необходимо использовать в системе вариативные по формулировке задачи (объясни, проверь, оцени, выбери, сравни, докажи, найди закономерность, верно ли утверждение, догадайся, наблюдай, сделай вывод, докажи, опровергни и т.д.), которые нацеливают учащихся на применение различных умений, входящих в структуру действия «прогнозирования».

Для того, чтобы набор задач стал системой, необходимо соблюдение определенных принципов конструирования, таких как: целостность, структурность, целенаправленность, интегративность, иерархичность [9]. Сконструированная система задач схематично представлена на рис.1.

Целостность системы определяется тем, что по структуре своей она состоит из более мелких подсистем и элементов. Одна подсистема – это группа задач любого из трех представленных выше уровней. Элемент – это задача любого уровня сложности.

Структурность системы подразумевает наличие определенных связей между подсистемами системы. На схеме это наглядно проиллюстрировано.  При решении задач по геометрии, как правило, формируется одно и более умений одновременно, это  делает компоненты взаимосвязанными.

Вся система задач направлена на формирование действия «прогнозирования», то есть действие системы подчинено одной цели. Так обеспечивается целенаправленность системы.

Интегративность  предполагает наличие системообразующих факторов. Такими системообразующим фактором мы считаем задачи, трех уровней: «простейшие задачи», «задачи для каждой группы умений», «интегрированные задачи». Они от уровня к уровню усложняются, чем вызывают у ученика необходимость применять умения или группы умений в совокупности.

Иерархичность системы обозначает, что каждый ее компонент может рассматриваться как отдельная подсистема. Это свойство обеспечивает наличие трех уровней задач, дифференцированных по необходимости применения определенных умений и по уровню сложности.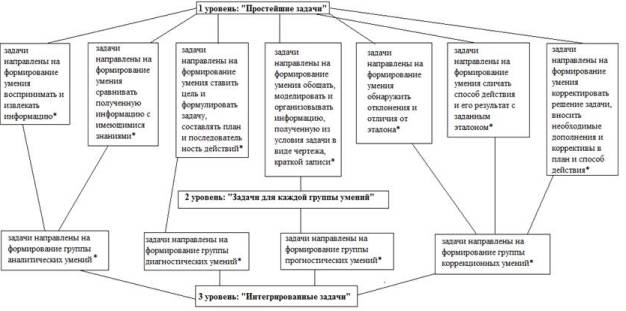

Рис.1. Схема системы задач по геометрии, направленная на формирование действия "прогнозирование". 
*) задачи разделены на три уровня сложности

Система задач по геометрии, сконструированная нами, организована по уровневому принципу и обладает всеми свойствами системы: целостность, структурность, целенаправленность, интегративность, иерархичность. Цель системы – формирование действия «прогнозирования» при решении задач по геометрии в основной школе. Разработаны три уровня задач: первый - «простейшие задачи», второй - «задачи для каждой группы», третий - «интегрированные задачи».  Блок из задач каждого уровня представляет собой единицу системы задач.

Литература:

1. Балл Г.А. Теория учебных задач: Психолого-педагогический аспект / Г.А. Балл. – М.: Педагогика, 1990. – 184 с.

2.  Гальперин П.Я. Методы обучения и умственное развитие ребенка / П.Я. Гальперин. – М.: Изд-во Московского университета, 1985.– 45 с.

3. Давыдов В. В. и др. Организация развивающего обучения в V-IX классах средней школы //Психологическая наука и образование. – 1997 - № 1. – С. 22-27.

4. Давыдов В.В. Психологическая теория учебной деятельности методов начального обучения, основанных на содержательном обобщении/ В.В. Давыдов. – Томск: Пеленг, 1992, – 116с

5. Демидович Е.А. Учебные задачи как средство формирования оценочной самостоятельности младших школьников в процессе обучения математике: дис. ... канд. пед. наук: 13.00.02/ Демидович Елена Анатольевна. – Омск, 2011.– 26 с.

6. Максютин А.А. Многоуровневая система задач как средство обучения учащихся средней школы алгебре и началам математического анализа: автореф. … канд. пед. наук: 13.00.02/ Максютин Алексей Алексеевич. – Самара, 2007. – 24с.

7. Машбиц Е.И. Психолого-педагогические проблемы компьютеризации обучения: – М.: Педагогика, 1988.–192 с.

8. Столяр А. А. Педагогика математики/ Под ред. А. А. Столяра - Минск: "Вышэйшая школа", 1986. С. 149-150.

9. Садовский В. Н. Основания общей теории систем/ Под ред.  А. И. Уемова – Москва: «Наука», 1974. С. 83-104.

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

________________

Olga V. Bolukh 
Postgraduate student, Department of Teaching methods in Mathematics  and  Informatics, Al.Herzen State Pedagogical University  of Russia, St. Petersburg
bolukholga@mail.ru

Victoria I. Snegurova
Doctor of Pedagogical Sciences, Professor,  Department of Teaching methods in Mathematics  and  Informatics, Al.Herzen State Pedagogical University  of Russia, St. Petersburg
kafedra.mom@gmail.com  

System requirements tasks, contributing to the formation of the action of “prediction” 

This article designed a system of tasks aimed at the formation of the action "prediction" in the process of teaching of geometry in primary schools, and presented in the form of a diagram; formulate the requirements to the contents of the given system of tasks.

Keywords:
system problems in mathematics, the requirements for system tasks, system construction tasks 

Literatura

1. Score, G. A. the Theory of educational objectives: Psycho-pedagogical aspects / A. G. Score. – M.: Pedagogika, 1990. – 184 p.

2. Galperin, P. Y. Methods of teaching and mental development of the child / P. J. Halperin. – M.: Publishing house of Moscow University, 1985.– 45 C.

3. Davydov V. V., Organization of developmental education in the V-IX classes of high school //Psychological science and education. – 1997 - No. 1. – P. 22-27.

4. Davydov, V. V. the Psychological theory of learning activity of primary methods of learning based on meaningful generalization/ V. V. Davydov. – Tomsk: Bearing, 1992, – s

5. E. A. Demidovich Learning objectives as a means of formation evaluation independence of younger school students in learning mathematics: dis. ... candidate. PED. Sciences: 13.00.02/ Demidovich Elena. – Omsk, 2011.– 26 C.

6. Maksiutin, A. A. a multi-level system tasks as a teaching tool for high school students algebra and the beginnings of mathematical analysis: author. ... candidate. PED. Sciences: 13.00.02/ Maksyutin Alexei. – Samara, 2007. – 24C.

7. Mashbits, E. I. Psychological and pedagogical problems of computerization of education: – M.: education, 1988.-192 C.

8. Stolyar A. A. Pedagogy of mathematics/ ed. by A. A. Carpenter - Minsk: "higher school", 1986. P. 149-150.

9. Sadovsky V. N. The Foundation of General systems theory/ edited by A. I. Uyomov – Moscow: "Nauka", 1974. P. 83-104.