Abstract
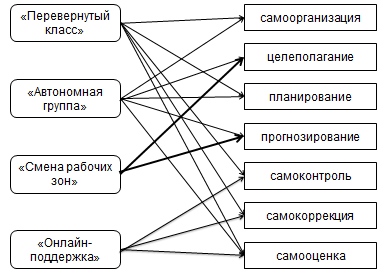
The article indicates what opportunities the structural elements of blended learning have for the development of regulative universal educational actions (UEA) of primary school students. The correspondence between the models of blended learning in mathematics and the content components of regulative UEA, from the perspective of a developmental orientation, has been established.

Key words: regulative universal educational actions, blended learning, models of blended learning, teaching mathematics.

----------------

В современном мире человеку недостаточно однажды приобретенных знаний и навыков, ему приходится постоянно совершенствоваться, изучать новое, т.е. сегодняшний школьник должен быть готов к самоорганизации процесса собственного развития. Поэтому педагогу важно уже обучающихся основной школы, когда естественно стремление к самостоятельности, обостряется необходимость самоопределения, самореализации [1, с.328], снабдить обучающихся механизмами саморегуляции, помочь в организации собственной учебной деятельность. Снятие данных потребностей отражено в Федеральных государственных образовательных стандартах и сопряжено с развитием регулятивных универсальных учебных действий (УУД).

Рассмотрим потенциал технологии смешанного обучения для решения задач формирования и развития регулятивных УУД при обучении математике обучающихся основной школы. Под смешанным обучением будем понимать модель электронного обучения, представимую через разделение и последующее совмещение синхронных и асинхронных форматов взаимодействия педагога и обучающихся, при обязательном самообразовании последних [2, 3, 4]. В исследованиях Г.Н. Гиматдиновой [5], Л.В. Шкериной [6], Т.П. Фисенко [3, 4] раскрываются отдельные аспекты, указывающие на возможности смешанного обучения математике для развития регулятивных УУД. Однако следует уточнить содержательные компоненты регулятивных УУД с учетом наличия асинхронного режима работы обучающихся, установить соответствие между такими компонентами и моделями смешанного обучения, способствующих их непосредственному проявлению в процессе обучения математике.

В обновленном варианте Федеральных государственных образовательных стандартов основного общего образования к универсальным регулятивным действиям (или регулятивным УУД в предыдущем варианте стандартов) относятся учебные действия, включающие способность принимать и сохранять учебную цель и задачу, планировать ее реализацию, контролировать и оценивать свои действия, вносить соответствующие коррективы в их выполнение, ставить новые учебные задачи, проявлять познавательную инициативу в учебном сотрудничестве, осуществлять констатирующий и предвосхищающий контроль по результату и способу действия, актуальный контроль на уровне произвольного внимания [7].

Выделенные в стандарте действия, уточняют содержательные компоненты регулятивных УУД, традиционно выделяемые в психолого-педагогической литературе: целеполагание, планирование, прогнозирование, контроль, оценка, коррекция и саморегуляция [8, 9]. В условиях электронного обучения, в частности дистанционного, отдельные компоненты универсальных регулятивных действий дополняются словообразовательной единицей «само-»: самооценка, самоконтроль, самокоррекция [10]. Наряду с этим, в примерной рабочей программе основного общего образования «Математика», размещенной на сайте Министерства просвещения РФ [11], в качестве универсальных регулятивных действий указываются только самоорганизация и самоконтроль. При этом в их составе отмечаются действия, которые находят отражение практически во всех обозначенных выше компонентах регулятивных УУД, скорректированные с учетом предметной области «Математика» для основной школы и сгруппированные в отдельные блоки. Таким образом, с учетом отмеченных уточнений, в качестве содержательных компонентов регулятивных УУД будем выделять: самообразование, целеполагание, планирование, прогнозирование, самоконтроль, самокоррекция, самооценка.

Среди моделей смешанного обучения математике нами выбраны такие, как «Перевернутый класс», «Автономная группа», «Онлайн-поддержка» («Аудиторное обучение с онлайн-поддержкой»). Данные модели требуют наименьшего изменения в пространстве класса, времени работы с электронными (цифровыми) ресурсами, учитывают недостаточное оснащение учебных заведений компьютерным оборудованием с современным программным обеспечением, а также позволяют учителю не терять связь со всем классом, гибко выстраивая свою позицию [4]. Также среди популярных моделей смешанного обучения в России выделяется «Смена рабочих зон», когда весь класс делится на группы и у каждой из них может стоять свои задачи [2, c. 69]. Использование данной модели также представляет особый возможности для развития регулятивных УУД. Внедрение различных моделей смешанного обучения позволяет акцентировать внимание на том или ином компоненте регулятивных действий. Результат установления соответствия между содержательными компонентами регулятивных УУД и выделенными моделями смешанного обучения, которые в большей степени нацелены на развитие этих компонентов, представлен на рисунке 1.

Рис. 1. Направленность моделей смешанного обучения на развитие компонентов регулятивных УУД

Стрелками указаны только те связи, для которых проявление того или иного компонента регулятивных УУД является наиболее естественным и логичным. Однако, это не означает, что те или иные модели не направлены на развитие других универсальных регулятивных действий. В то же время, математика, как предметная область имеет ряд особенностей, связанных с развитием регулятивных УУД в условиях смешанного обучения. Обучение математике преимущественно строится через задачи, новый учебный материал требует обращения к предыдущему опыту, опоры на имеющиеся знания, на установления аналогий и т.п. За счет обозначенных характеристик данного учебного предмета в условиях смешанного обучения возможно говорить о целенаправленном и планомерном развитии регулятивных действий обучающихся.

Самоорганизация. Модели «Перевернутый класс», «Автономная группа» сразу нацеливают обучающих на самостоятельную организацию рабочего места при изучении цифрового контента, в том числе для фиксации основных сведений, выполнения вычислений, а также указания степени поддержки при работе с пакетами математических программ. Работая в асинхронном режиме, обучающиеся сами определяют достаточное количество типовых задач.

Целеполагание. Цель формулируется после того, как обучающиеся сталкиваются с проблемой, например, осознают недостаточность имеющихся знаний и умений при выполнения новых заданий (переход от уравнений определенного вида к соответствующим неравенствам, от частного вида функции к более общему, от действий с обыкновенными дробями к действиям с рациональными и т.д.). Решение такой проблемы рациональней выполнять не отдельно, а в группе, сформированной с учетом индивидуальных особенностей обучающихся, что возможно в условиях моделей «Смена рабочих зон» и «Автономная группа». Последняя из них предполагает также осуществление целеполагания без помощи учителя, т.к. небольшая часть класса выполняет задание, отличное от остальных.

Планирование. Перед выполнением работы в асинхронном режиме в рамках модели «Перевернутый класс» обучающимся необходимо самостоятельно определить сроки, продолжительность, глубину, последовательность освоения учебных блоков, а «Автономная группа» также предполагает распределение обязанностей внутри группы, форму представления отчета, полноту проработки вопроса и т.д. В синхронном режиме составляется план работе всего класса на урок, а также определяется или проверяется последовательность шагов при выполнении математических заданий (алгоритм решения задачи, этапы исследования, порядок выполнения действий и т.п.).

Прогнозирование. Организация группового сотрудничества в условиях моделей «Автономная группа» и «Смены рабочих зон» нередко предусматривает проведение математических компьютерных экспериментов, что подводит обучающихся к анализу различных вариантов, предвидению результатов, выдвижению гипотез. Обоснование предположение возможно при синхронном формате взаимодействия.

Самоконтроль и самокоррекция. В рамках моделей «Перевернутый класс» и «Онлайн-поддержка» обучающиеся должны сами определить правильность понимания изученного материала (дома самостоятельно или в классе с учителем), выполнения и записи отдельных шагов решения, точности полученных результатов, к тому же в случае необходимости они должны получить своевременную реакцию на ошибку. Для этих целей предусматривается использование обучающих тестов, интерактивных лекций и заданий, которые направляют, указывают на ошибку, демонстрируют шаблон решения, а также позволяют вернуться к теоретическому материалу, который необходимо повторить, не позволяют перейти к заданиям следующего уровня, пока ошибка не будет устранена, осознана. Поэтому с целью самокоррекции лучше предлагать задания открытого типа (записать ответ, заполнить пропуски, указать возможные значения и т.д.), с наличием подсказок, в случае затруднений. При проверке правильности выполнения задания можно также использовать возможности математических программ (графический калькулятор при построении графиков функции, онлайн калькулятор для математических расчетов и т.д.).

Самооценка. Наряду с моделями «Перевернутый класс» и «Онлайн-поддержка», условия модели «Автономной группы» способствуют подведению обучающихся к оцениванию проделанной работы в асинхронном режиме. Обучающиеся могут оценивать свои знания исходя из количества правильно выполненных заданий, критерий же для этого предлагает педагог. Однако, здесь важно, чтобы ученик сам оценил, например, по десятибалльной шкале, уровень понимания учебного материала, собственное усердие в освоении нового, степень самостоятельности, насколько ему было интересно, сложно работать. Для получения оперативных результатов опрос следует осуществлять посредством заполнения электронных таблиц, онлайн форм.

Смешанное обучение направляет на выполнение действий, соответствующих разным аспектам регулятивной деятельности обучающихся. Так, при синхронном формате взаимодействия учитель нацеливает ребят на необходимость выполнения действий, связанных с общей организацией учебного процесса, отмечает, как они могут быть достигнуты (совместное целеполагание, планирование), работает с теми обучающимися, которые еще недостаточно готовы к самостоятельному решению отдельных учебных задач, вместе с ними выполняет проверку и при необходимости коррекцию предметных знаний и умений, приобретенных школьниками, в том числе и при асинхронной работе. В асинхронном режиме  действия учеников выполняются без непосредственного контроля со стороны педагога, ученики сами выбирают объем заданий, их характер, проверяют, контролируют правильности понимания того или иного учебного материала с помощью интерактивных заданий. Элемент «самообразование», который является частью модели смешанного обучения,  указывает на связь с регулятивной составляющей деятельности ученика. Обучающемуся  указали обязательные пункты работы, но не ограничили, создавая при этом условия для продвижения в освоении предмета. При этом учителям следует учитывать степень предметных знаний, скоростью усвоения учебного материала, учебную мотивацию обучающихся.

Таким образом, смешанное обучение математике имеет определенный потенциал для развития регулятивных УУД обучающихся. Особую значимость в этом процессе приобретают различные сочетания асинхронного и синхронного режимов работы в разных моделях смешанного обучения. Представляется, что  обозначенные в статье  идеи о возможностях смешанного обучения для развития регулятивных действий могут быть адаптированы и для других дисциплин с учетом их специфики.

Литература

1. Фельдштейн Д.И. Психология взросления: структурно-содержательные характеристики процесса развития личности. – М.: Моск. психолого-социальный ин-т: Флинта, 1999. – 672 с.

2. Дидактико-методические основы смешанного обучения математике в школе: монография / В.А. Далингер, М.В. Дербуш, Р.Ю. Костюченко [и др.]. – Омск: Изд-во ОмГПУ, 2021. – 244с.

3. Фисенко Т.П. Возможности смешанного обучения математике для развития регулятивных универсальных учебных действий обучающихся // Вестник Сибирского института бизнеса и информационных технологий. – 2021. – Т. 10, № 3. – С. 50–58.

4. Фисенко Т.П. Синхронные и асинхронные составляющие смешанного обучения математике // Познание и деятельность: от прошлого к настоящему: материалы III Всероссийской междисциплинарной научной конференции / отв. ред. И.П. Геращенко – Омск: Изд-во ОмГПУ, 2021. – С.150-153.

5. Гиматдинова Г.Н. Возможности использования онлайн-сервиса «ЯКласс» для формирования регулятивных универсальных учебных действий обучающихся 7-9 классов // Концепт. – 2020. – № 8. – С.87-99.

6. Гиматдинова Г.Н., Шкерина Л.В. Дидактический потенциал смешанного обучения математике обучающихся 7-9-х классов для формирования регулятивных универсальных учебных действий // Вестник Красноярского государственного педагогического университета им. В.П. Астафьева. – 2022. – 60(2). – С. 13-23.

7. Приказ Министерства просвещения Российской Федерации от 31.05.2021 № 287 «Об утверждении федерального государственного образовательного стандарта основного общего образования». URL: http://publication.pravo.gov.ru/Document/View/0001202107050027?index=0&rangeSize=1/ [Дата обращения 01.12.2022]

8. Асмолов А.Г., Бурменская Г.В., Володарская И.А. и др. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя. – М.: Просвещение, 2010. – 159 с.

9. Голубчикова М.Г., Голубчиков Г.М., Федотова Е.Л. Формирование регулятивных универсальных учебных действий школьников – основа развития самостоятельности личности // Наука о человеке: гуманитарные исследования. – 2020. – №4. – С.91-99.

10. Поберезкая В.Ф., Новикова Н.Н. Диагностика регулятивных универсальных учебных действий обучающихся в условиях дистанционного обучения // Концепт. – 2021. – №5. – С. 84-99.

11. Примерная рабочая программа основного общего образования. Математика. Базовый уровень (для 5-9 классов общеобразовательных организаций). Москва, 2021. URL: https://fgosreestr.ru/oop/primernaia-rabochaia-programma-osnovnogo-obshchego-obrazovaniia-matematika [Дата обращения 01.12.2022]

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

Literature

1. Fel'dshtejn D.I. Psihologiya vzrosleniya: strukturno-soderzhatel'nye harakteristiki processa razvitiya lichnosti. – M.: Mosk. psihologo-social'nyj in-t: Flinta, 1999. – 672 s.

2. Didaktiko-metodicheskie osnovy smeshannogo obucheniya matematike v shkole: monografiya / V.A. Dalinger, M.V. Derbush, R.YU. Kostyuchenko [i dr.]. – Omsk: Izd-vo OmGPU, 2021. – 244 s.

3. Fisenko T.P. Vozmozhnosti smeshannogo obucheniya matematike dlya razvitiya regulyativnyh universal'nyh uchebnyh dejstvij obuchayushchihsya // Vestnik Sibirskogo instituta biznesa i informacionnyh tekhnologij. – 2021. – T. 10, № 3. – S. 50–58.

4. Fisenko T.P. Sinhronnye i asinhronnye sostavlyayushchie smeshannogo obucheniya matematike // Poznanie i deyatel'nost': ot proshlogo k nastoyashchemu: materialy III Vserossijskoj mezhdisciplinarnoj nauchnoj konferencii / otv. red. I.P. Gerashchenko – Omsk: Izd-vo OmGPU, 2021. – S.150-153.

5. Gimatdinova G.N. Vozmozhnosti ispol'zovaniya onlajn-servisa «YAKlass» dlya formirovaniya regulyativnyh universal'nyh uchebnyh dejstvij obuchayushchihsya 7-9 klassov // Koncept. – 2020. – № 8. – S.87-99.

6. Gimatdinova G.N., SHkerina L.V. Didakticheskij potencial smeshannogo obucheniya matematike obuchayushchihsya 7-9-h klassov dlya formirovaniya regulyativnyh universal'nyh uchebnyh dejstvij // Vestnik Krasnoyarskogo gosudarstvennogo pedagogicheskogo universiteta im. V.P. Astaf'eva. – 2022. – 60(2). – S. 13-23.

7. Prikaz Ministerstva prosveshcheniya Rossijskoj Federacii ot 31.05.2021 № 287 «Ob utverzhdenii federal'nogo gosudarstvennogo obrazovatel'nogo standarta osnovnogo obshchego obrazovaniya». URL: http://publication.pravo.gov.ru/Document/View/0001202107050027?index=0&rangeSize=1/ [Data obrashcheniya 01.12.2022]

8. Asmolov A.G., Burmenskaya G.V., Volodarskaya I.A. i dr. Formirovanie universal'nyh uchebnyh dejstvij v osnovnoj shkole: ot dejstviya k mysli. Sistema zadanij: posobie dlya uchitelya. – M.: Prosveshchenie, 2010. – 159 s.

9. Golubchikova M.G., Golubchikov G.M., Fedotova E.L. Formirovanie regulyativnyh universal'nyh uchebnyh dejstvij shkol'nikov – osnova razvitiya samostoyatel'nosti lichnosti // Nauka o cheloveke: gumanitarnye issledovaniya. – 2020. – №4. – S.91-99.

10. Poberezkaya V.F., Novikova N.N. Diagnostika regulyativnyh universal'nyh uchebnyh dejstvij obuchayushchihsya v usloviyah distancionnogo obucheniya // Koncept. – 2021. – №5. – S. 84-99.

11. Primernaya rabochaya programma osnovnogo obshchego obrazovaniya. Matematika. Bazovyj uroven' (dlya 5-9 klassov obshcheobrazovatel'nyh organizacij). Moskva, 2021. URL: https://fgosreestr.ru/oop/primernaia-rabochaia-programma-osnovnogo-obshchego-obrazovaniia-matematika [Data obrashcheniya 01.12.2022]