Аннотация
В статье отражены основные результаты исследовательской деятельности, целью которой стала экспериментальная проверка эффективности предложенных методических приемов реализации преемственности в обучении математическому анализу в вузе. В рамках исследования реализовывался педагогический эксперимент для проверки выдвинутой гипотезы, а полученные результаты достоверно свидетельствуют об ее подтверждении.

Ключевые слова: математический анализ, преемственность в обучении, теория и методика обучения математике.

----------------

Anna F. Veselova
Junior Researcher, Scientific and Educational Mathematical Center "North-Western Center for Mathematical Research named after Sofia Kovalevskaya", Pskov State University, Pskov
af.veselova@pskgu.ru

Valentin N. Melnik
Candidate of Physical and Mathematical Sciences, Head of the Department of Applied Informatics and Modeling, Pskov State University, Pskov
melnik@pskgu.ru

Some techniques for implementing continuity in teaching mathematical analysis at a university

Abstract
The article reflects the main results of research activities, the purpose of which was to experimentally test the effectiveness of the proposed methodological techniques for implementing continuity in teaching mathematical analysis at a university. As part of the study, a pedagogical experiment was carried out to test the hypothesis put forward, and the results obtained reliably indicate its confirmation.

Key words: mathematical analysis, continuity in teaching, theory and methods of teaching mathematics.

----------------

Преемственность в обучении – это важное понятие, связанное с плавным переходом студентов из школы в вуз и обеспечением непрерывности образовательного процесса. Возникающие методические проблемы в этой сфере требуют внимания и поиска эффективных решений. Одной из основных проблем преемственности является разрыв между школьной и вузовской программами по математике. Школьная программа ориентирована на общее развитие учащихся, в то время как вузовская программа более узкоспециализирована и требует глубоких знаний в определенной области. Это может создавать сложности для студентов, которые не всегда готовы к такому переходу. Кроме того, проблемы могут возникать из-за различий в формах организации учебного процесса и оценки знаний обучающихся. В школе акцент часто делается на запоминании и повторении информации, в то время как в вузе требуется аналитическое мышление и самостоятельная работа. Это может вызывать трудности у студентов, которые не привыкли к такому подходу.

Одним из возможных решений проблемы преемственности может быть более тесное сотрудничество между школами и вузами. Например, курсы подготовки к ЕГЭ, математические кружки, математические школы, курсы повышения квалификации для учителей математики. Также важно обратить внимание на то, что психологически первокурсники не готовы к новым условиям обучения, требуется период адаптации.

Математический анализ является одной из фундаментальных учебных дисциплин естественно-математического профиля. Математический анализ позволяет понять и описать различные явления и процессы в природе, экономике, физике и других дисциплинах с помощью математических моделей. Соколова А.А. [1] считает, что в математическом анализе, как и в других дисциплинах, невозможно изучать новые темы в случае, если предыдущие были не поняты. Кошназаров Р.А. [2] отмечает, что успешность понимания основ математического анализа в вузе зависит от того, насколько хорошо первокурсник владеет понятиями и их свойствами, изученными в школьном курсе начал анализа, а также учебными действиями общего и частного характера.

Реализация содержательной преемственности в обучении математическому анализу - важный аспект в образовании. Это способствует эффективному усвоению и пониманию материала, создавая новые связи с уже изученными. Они помогают студентам установить связь между новыми и школьными знаниями, что способствует более глубокому пониманию математического анализа. Кроме того, реализация преемственности позволяет студентам увидеть целостность и логическую последовательность теории математического анализа.

Преемственность также способствует формированию мотивации студентов к изучению сложной дисциплине – математический анализ. Они осознают, что это не просто набор теорем и формул, а целостная система знаний, которая имеет большой спектр практического применения.

Преемственность в обучении математическому анализу может быть реализована через следующие приемы:

1. Актуализация математического школьного материала, систематизация знаний.

2. Использование аналогий.

3. Постепенное усложнение задач.

4. Интеграция теории и практики.

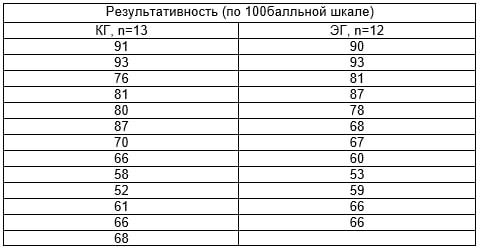
Опираясь на результаты теоретического анализа результатов, представленных в исследовательских работах авторов в контексте настоящей работы и цели, а также собственный практический опыт, накопленный в образовательной практике, предложены методические приемы, обеспечивающие преемственность в обучении математическому анализу:

Оценка эффективности подразумевает повышение результирующих показателей по курсу математического анализа у студентов первокурсников по направлению подготовки «Прикладная информатика» (n=25 человек) двух групп – экспериментальной (ЭГ, n=12 человек) и контрольной (КГ, n=13 человек). В ходе реализации курса математического анализа в обеих группах существовало различие, которое заключалось в отсутствии методических приемов в КГ, которые предлагались для студентов в ЭГ.

Длительность экспериментальной части исследования составляла 3 месяца, на протяжении которой КГ обучалась по традиционной методике обучения, а в ЭГ использовалась вышеобозначенная методика преемственности в обучении математическому анализа в рамках существующей рабочей программы по дисциплине «Математический анализ».

Экспериментальная деятельность, реализуемая в рамках образовательного процесса, включала в себя педагогический эксперимент, объединяющий в себе констатирующий формирующий и контрольный этапы. В рамках констатирующего этапа педагогического эксперимента были зафиксированы показатели входного контроля знаний по дисциплине математический анализ в обеих группах (см. таблицу 1).

Таблица 1

Исходный уровень знаний по дисциплине математический анализ, констатирующий этап педагогического эксперимента

Из-за малочисленности объемов и независимости выборок КГ и ЭГ, для проверки их однородности мы использовали непараметрический критерий Манна-Уитни (пакет Statistica 10). На констатирующем этапе педагогического эксперимента в качестве нулевой гипотезы принимается гипотеза об отсутствии различий в уровне знаний по дисциплине «Математический анализ» в КГ и ЭГ. Результаты плаченного теста приведены на Рисунке 1.

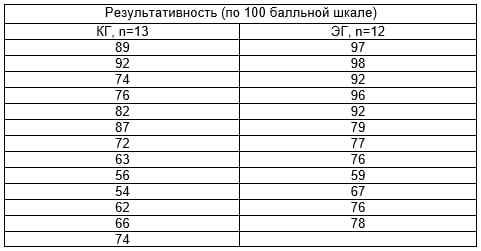
Рис. 1. Результат сравнения результативности КГ и ЭГ на констатирующем этапе педагогического эксперимента с помощью теста Манна-Уитни

Поскольку асимптотическое двустороннее p-значение 0,891545 > 0,05, мы не можем отвергнуть нулевую гипотезу. Таким образом на 5% уровне статистической значимости принимается гипотеза об однородности КГ и ЭГ.

В рамках формирующего этапа экспериментальной части исследования осуществлялась реализация учебного процесса в обеих группах студентов. По окончанию формирующего этапа были осуществлены повторные измерения, фиксируемые в протоколах преподавателями и представлены в таблице 2.

Таблица 2

Результаты освоения дисциплины математический анализ на контрольном этапе педагогического эксперимента

Для проверки статистической значимости результатов на контрольном этапе педагогического эксперимента также использовался критерий Манна-Уитни. Результаты которого приведены на Рисунке 2.

Рис. 2. Результат сравнения результативности КГ и ЭГ контрольном этапе педагогического эксперимента с помощью теста Манна-Уитни

Поскольку асимптотическое двустороннее p-значение 0,046726 < 0,05, мы можем отвергнуть нулевую гипотезу об отсутствии различий в уровне освоения знаний по дисциплине «Математический анализ» в КГ, которая занималась по традиционной методике и ЭГ, в которой была применена методика реализации преемственности. Таким образом на 5% уровне статистической значимости принимается альтернативная гипотеза о различие в результатах КГ и ЭГ.

Полученные результаты свидетельствуют об эффективности комплекса предложенных методических приемов, что дает основание для рекомендации их использования в образовательном процессе вуза по дисциплине математического анализа.

Литература

1. Соколова А.А. Особенности преподавания математического анализа студентам первого курса математического факультета // Материалы IX Международной студенческой научной конференции «Студенческий научный форум». URL: https://scienceforum.ru/2017/article/2017031638 [Дата обращения 09.01.2024]

2. Кошназаров, Р. А. Обучение математическому анализу студентов первого курса в контексте деятельностного подхода / Р. А. Кошназаров, М. Н. Жураева. — Текст : непосредственный // Молодой ученый. 2014. № 10 (69). С. 392-394. URL: https://moluch.ru/archive/69/11818/ [Дата обращения 09.01.2024]

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

Literature

1. Sokolova A.A. Osobennosti prepodavaniya matematicheskogo analiza studentam pervogo kursa matematicheskogo fakul'teta // Materialy IX Mezhdunarodnoj studencheskoj nauchnoj konferencii «Studencheskij nauchnyj forum». URL: https://scienceforum.ru/2017/article/2017031638 [Data obrashcheniya 09.01.2024]

2. Koshnazarov, R. A. Obuchenie matematicheskomu analizu studentov pervogo kursa v kontekste deyatel'nostnogo podhoda / R. A. Koshnazarov, M. N. Zhuraeva. — Tekst : neposredstvennyj // Molodoj uchenyj. 2014. № 10 (69). S. 392-394. URL: https://moluch.ru/archive/69/11818/ [Data obrashcheniya 09.01.2024]