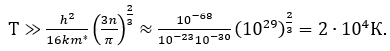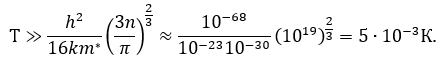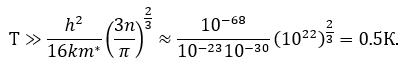| |||||
|
The Emissia.Offline Letters Электронное научное издание (педагогические и психологические науки) | |||||
|
Издается с 7 ноября 1995 г. Учредитель: Российский государственный педагогический университет им. А.И.Герцена, Санкт-Петербург | |||||
|
|||||
|
_________ Шифр научной специальности 5.8.2. Доронин Вячеслав Александрович Щедровский Александр Анатольевич
Аннотация Ключевые слова: инженерное образование, практико-ориентированное образование; проектно-исследовательская деятельность, профессионально-значимые компетенции, физика полупроводников. ---------------- Vyacheslav A. Doronin Alexander A. Shchedrovsky
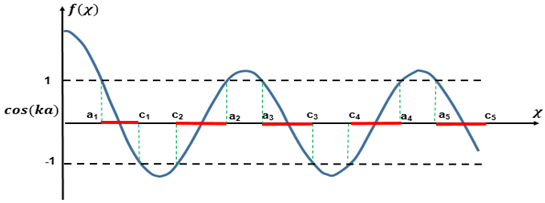
Abstract Key words: engineering education, practice-oriented education; project-based research activities, professionally significant competencies, semiconductor physics. ---------------- Физическое моделирование свойств материалов, а также протекающих в них физических процессов – это творческий процесс требующий длительного обучения. Будущие инженеры должны обладать умениями физического моделирования при решении исследовательских задач. Формирование данных умений построения физических моделей у обучающихся требует от системы подготовки разработки методических подходов практико-ориентированного обучения важных для будущей профессиональной деятельности разделов физики [1, 2]. Одним из таких разделов выступает физика конденсированного состояния. В работе отражены значимые для описания функциональных свойств кристаллов модели физики конденсированного состояния, рассмотрены границы их применимости. Рассмотрим ряд фундаментальных физических моделей используемых в физике твердого тела, физике полупроводников, играющих важную роль в процессе специализации обучающихся в предметной области твердотельной микро- и наноэлектроники. В физике твердого тела одной из основных задач выступает определение энергетического спектра носителей заряда в кристаллах, что представляется сложной квантово-механической задачей. Понимание особенностей энергетического спектра электронов в различных материалах является значимым для анализа функциональных свойств элементов микроэлектроники на их основе. В связи с этим в процессе подготовки обучающихся необходимо провести анализ фундаментальной квантово-механической модели твердого тела (модель Кронига-Пенни) [3], в которой рассматривается движение электрона в периодическом потенциальном поле, состоящем из бесконечной последовательности квантовых ям и барьеров шириной b и высотой U0. В ходе рассмотрения данной модели решается стационарное уравнение Шредингера и обучающиеся приходят к уравнению:
где k – квантовое число (связано с квазиимпульсом электрона p=hk),
определяющее трансляционные свойства волновой функции ψ; a- ширина
квантовых ям, отделенных друг от друга барьерами; χ – коэффициент,
связанный с энергией электрона
Рис.1. Графическое решение обобщенного уравнения (1) В точках [a1 c1], [c2 a2], [a3 c3], [c4 a4] представленное уравнение имеет решение, график при этом похож на “разорванную” параболу и показывает связь энергии частицы (E) с её импульсом (p) или волновым числом (k). Проведя анализ данной модели Кронига-Пенни обучающиеся осваивают фундаментальную основу возникновения разрешенных и запрещенных энергетических зон в кристаллах. Решение данной модели может быть обобщено и на трехмерный случай. Здесь обучающиеся узнают, что внутри разрешенных зон энергия электрона E(k) – непрерывная функция, а сами зоны могут частично перекрываться. Важными физическими моделями, на которые следует обратить глубокое внимание обучающихся при освоении функциональных свойств кристаллов (металлов, полупроводников) являются модели вырожденного и невырожденного электронного газа. Вырожденный электронный газ описывается квантовой функцией распределения Ферми-Дирака
в то время, как классический (невырожденный) электронный газ функцией распределения Максвелла-Больцмана
где µ-электрохимический потенциал. При сравнении обучающимися выражений (2) и (3) обнаруживается следующий вывод: при описании функциональных свойств материалов квантовая функция распределения в ряде случаев может быть заменена на классическую, если экспонента в (2) много больше единицы e(E-μ)/kT >> 1. В случае фермионов (электронов) это условие выполняется для энергий существенно больших энергии Ферми (µ=Eф). При описании таких частиц может быть выполнена замена функции Ферми-Дирака на функцию Максвелла-Больцмана. В качестве примера такой замены с обучающимися можно рассмотреть явление термоэлектронной эмиссии: из металла в ходе нагревания вылетают только те электроны, энергия которых на несколько электронвольт больше энергии Ферми. Еще одним критерием выбора модели электронного газа при описании свойств кристаллов является повышение температуры, при котором выполняется условие малости энергии Ферми Eф << 2kT. Обучающимся можно предложить переписать данное условие в другом виде, используя выражение связи энергии Ферми в кристаллах и концентрации электронов в них:
где где m* - эффективная масса электрона; n-концентрация электронов. Заменяя в этом выражении энергию Ферми на 2kT обучающиеся могут получить следующее неравенство
Полученное выражение представляет собой критерий перехода статистки Ферми-Дирака к статистике Максвелла-Больцмана (выбора модели электронного газа). Для того, чтобы весь электронный газ был невырожденным, то есть электроны были способны менять свои состояния при изменении температуры или включении электрического поля необходимо выполнение данного условия (5). Из представленного неравенства (5) обучающиеся делают вывод: переход к статистике Максвелла-Больцмана возможен при малых концентрациях частиц или при высоких температурах. В качестве примера рассмотрим изучение электронных свойств металлов в курсе физики твердого тела. Здесь обучающимся на практическом занятии можно предложить самим определить температуру перехода к статистике Максвелла-Больцмана. Для металлов в силу высоких концентраций электронов n~1029м-3 переход к статистике Максвелла-Больцмана возможен при температурах:
В этой связи в металлах при описании поведения электронного газа используется модель вырожденного электронного газа. Рассмотрим другой пример, в котором с обучающимися можно проанализировать поведение электронного газа в зоне проводимости собственного полупроводника. В полупроводниках концентрация электронов меняется в очень широком диапазоне значений. Для собственного германия, например, концентрация электронов при комнатной температуре составляет n~1019 м-3. С обучающимися можно провести расчет температуры снятия вырождения, которая здесь будет составлять:
В результате решения данной задачи обучающиеся узнают, что электронный газ в полупроводниках во всем диапазоне доступных температур описывается моделью невырожденного электронного газа, подчиняющегося статистике Максвелла-Больцмана. Даже при увеличении концентрации электронов в 103 раз в ходе изучения примесных полупроводников (например, легированных донорной примесью) расчеты показывают небольшое увеличение температуры снятия вырождения
Рассмотрение электронного газа как невырожденного подчиняющегося статистике Максвелла-Больцмана в слабо легированных полупроводниках возможно при температурах больших нескольких Кельвин. Акцентирование внимания обучающихся на применение физических моделей при решении образовательных и практических задач способствует приобретению у обучающихся важных когнитивных качеств личности:
Рекомендовано к публикации: Literature
| |||||
|
| |||||
| Copyright (C) 2025, Письма
в Эмиссия.Оффлайн (The Emissia.Offline Letters): электронный научный журнал ISSN 1997-8588 (online). ISSN 2412-5520 (print-smart), ISSN 2500-2244 (CD-R) Свидетельство о регистрации СМИ Эл № ФС77-33379 (000863) от 02.10.2008 от Федеральной службы по надзору в сфере связи и массовых коммуникаций При перепечатке и цитировании просим ссылаться на " Письма в Эмиссия.Оффлайн ". Эл.почта: emissia@mail.ru Internet: http://www.emissia.org/ Тел.: +7-812-9817711, +7-904-3301873 Адрес редакции: 191186, Санкт-Петербург, наб. р. Мойки, 48, РГПУ им. А.И.Герцена, корп.11, к.24а Издатель: Консультационное бюро доктора Ахаяна [ИП Ахаян А.А.], гос. рег. 306784721900012 от 07,08,2006. |
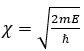 ; P-параметр барьера,
; P-параметр барьера,
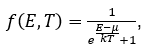 (2)
(2)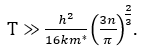 (5)
(5)