|
Ссылаться на эту работу следует следующим образом:
А.Г.Беленко. Диагностика образовательных результатов обучающихся на
основе учета их индивидуальных когнитивных особенностей // Письма в Эмиссия.Оффлайн (The Emissia.Offline Letters):
электронный научный журнал. 2022. №8 (август).
ART 3105. URL:
http://emissia.org/offline/2022/3105.htm
_________ Шифр научной специальности 05.08.02 (13.00.02)
Работа выполнена
при поддержке Российского фонда фундаментальных исследований (грант №
19-29-14080 мк). Финансирование проекта «Электронная система адаптивного
тестирования образовательных результатов по математике, информатике и
предметам естественно-научного цикла на основе когнитивных особенностей
обучающихся»
Беленко Алена Григорьевна
аспирант кафедры методики обучения математике и информатике, Российский
государственный педагогический университет им. А. И. Герцена,
Санкт-Петербург
belenko-ag@ranepa.ru
Диагностика образовательных результатов обучающихся на основе учета их
индивидуальных когнитивных особенностей
Аннотация
В статье рассматривается возможность учета индивидуальных стилей
кодирования информации обучающихся при диагностике образовательных
результатов по математике в старшей школе.
Проанализированы различные подходы к выделению уровней сложности
тестовых заданий. Определены основания выделения уровней в процессе
обучения математике: специфика деятельности ученика при работе с
информацией, необходимость применения материала для решения
практико-ориентированных задач, использование в задачах одного или
нескольких способов представления информации и требования перекодировать
её с одного способа на другой. Приведены примеры задач каждого уровня
сложности, построенные на основе учета индивидуальных особенностей
обучающихся.
Ключевые слова: уровни сложности задач, способы
представления информации, старшеклассники.
----------------
Alena G. Belenko
Postgraduate Student, Department of Methods of Teaching Mathematics and
Informatics, A.I. Herzen State Pedagogical University of Russia, St.
Petersburg
belenko-ag@ranepa.ru
Diagnostics of students’ learning outcomes on the basis of individual
cognitive characteristics
Abstract
The article deals with the possibility of accounting for students’
individual information coding style when diagnosing learning outcomes in
mathematics in high school. The study investigates different approaches
to the allocation of complexity levels of textual tasks. The research
highlights 4 levels of complexity of textual tasks according to 1) the
specifics of the student’s activity when working with the information,
2) the need to use the material for solving practice-oriented tasks, 3)
the use of one or more ways of presenting information in tasks and the
need to recode it from one way to another. The article gives the
examples of tasks of different complexity levels, based on individual
characteristics of the students.
Key words: task complexity levels, information coding style,
high school students.
----------------
Одной из основных задач модернизации современного образования
является его гуманизация. Гуманизация образования предполагает создание
условий для развития личности обучающихся, что влечет за собой изменение
методов и приемов работы с учениками. В связи с этим, важнейшим путем
реализации учебного процесса является его индивидуализация.
Индивидуализация обучения представляет собой такую модель организации
учебного процесса, при которой выбор способов, приемов, темпа обучения
обусловливается индивидуальными особенностями учащихся [1]. При обучении
математике эти особенности связаны, в первую очередь, с когнитивными
особенностями. Как считает М.А. Холодная, когнитивные стили представляют
собой частную форму индивидуальных познавательных стилей, которые
характеризуют индивидуально-своеобразные способы изучения реальности.
Одним из видов таких познавательных стилей являются стили кодирования
информации. Под стилями кодирования информации будем понимать
субъективные средства, с помощью которых развивающийся человеческий
индивид представляет (отображает) в своем опыте окружающий мир и которые
он использует в целях организации этого опыта для будущего поведения
[2]. Исследования В.А. Крутецкого [3], И.С. Якиманской [4] показывают,
что у обучающихся одного и того же возраста существуют различия в
способах кодирования(представления) информации: одни учащиеся легче
усваивают материал, представленный в виде математических символов,
другие - в виде геометрических фигур и рисунков, третьи – в виде
словесных формулировок. В федеральном государственном образовательном
стандарте говорится о необходимости развития умения перерабатывать
информацию для получения требуемого результата и преобразовывать ее из
одной формы представления в другую. О важности формирования умения
работать с информацией говорится и в международных исследованиях PISA.
Всё вышесказанное объясняет необходимость использования задач,
представленных в символьной, образно-графической или
вербальной(словесной) форме в процессе обучения математике.
Индивидуально-стилевые особенности обучающихся влияют на успешность
решения задачи учеником в зависимости от способа кодирования информации.
В действительности, ученики не всегда выбирают задачи, текст которых
представлен в приоритетном для них способе кодирования. При этом задачи,
в которых требуется умение использовать разные способы представления,
способствуют повышению индивидуализации интеллектуальной деятельности
[5].
В связи с этим, нами была проанализирована психолого-педагогическая и
учебная литература на предмет использования задач на перекодирование
информации в учебном процессе. Проведенный анализ показал, что таких
работ немного. Так, например, исследования [6], [7], [8] посвящены
методике работы с такими задачами на этапах введения материала,
первичного и вторичного закрепления. В работе [9] изучается проблема
обучения учащихся умению перекодировать информацию. При этом
исследований, посвященных вопросам использования разных способов
кодирований информации на этапе диагностики и контроля знаний, нет.
Анализ школьных учебников алгебры и различных дидактических материалов к
ним показал, что большинство предложенных заданий для самостоятельных и
контрольных работ представлены в одном способе кодирования информации (в
основном, в символьном), что противоречит методике Бетти Лу Ливер о том,
что на этапе закрепления материала учащимся необходимо предлагать
задания в приоритетном для них способе кодирования [10]. Поэтому в
статье мы рассмотрим именно этап диагностики образовательных результатов
по математике с учетом различных способов кодирования информации. В этом
и будет состоять научная новизна нашего исследования.
Одним из компонентов диагностики образовательных результатов является
контроль. К наиболее эффективной и объективной форме контроля знаний и
умений относится тестирование. Чтобы отследить продвижение ученика в
развитии какого-либо умения, необходимо выделить уровни развития этого
умения, которым будут соответствовать уровни сложности заданий. В
процессе разработки тестовых заданий важно уметь правильно определить их
уровень сложности. Существуют различные подходы к определению уровней
сложности задач.
Так, авторы работ [11, 12, 13] считают, что задания должны быть
разделены на три уровня сложности: уровень А – задания, в которых
требуется лишь распознавание материала; уровень Б – задания, в которых
необходимо применять материал в стандартных ситуациях; уровень В –
задания, требующие творческого применения полученных знаний, возможно, в
нестандартных ситуациях. Кузнецов А.А. тоже выделяет три уровня
сложности, но описывает их более обобщенно, что затрудняет их применение
на практике: к заданиям первого уровня сложности относит «простые
тестовые задания», ко второму уровню сложности относятся тестовые
задания, включающие в себя понятия, предусмотренные школьной программой,
но имеющие сложное определение, к третьему – задания, содержащие
понятия, не предусмотренные минимальными требованиями к результатам
освоения дисциплины [14].
Таким образом, нет единой точки зрения как в вопросе о количестве
выделяемых уровней сложности, так и в понимании того, каким именно
требованиям должны соответствовать задачи того или иного уровня
сложности. Исходя из целей нашего исследования, в проанализированных
работах мы отметили, что недостаточно раскрыты следующие аспекты:
- отсутствует входной уровень, в котором бы проверялись базовые
теоретические знания учащихся, необходимые для выполнения заданий в
рамках конкретной темы. Знание определений, формул, правил, теорем
является основой для успешного решения математических задач;
- ни в одном из описанных уровней ничего не сказано о
практико-ориентированных задачах. Одним из требований Федерального
государственного образовательного стандарта является умение использовать
приобретенные знания и умения в повседневной жизни. В международных
исследованиях PISA также проверяется умение применять знания в различных
жизненных ситуациях. Результаты российских учащихся в исследовании PISA
говорят о том, что в целом растет доля учащихся, которые не достигают
необходимого уровня функциональной грамотности [15]. Это означает, что
необходимо уделять внимание проверке функциональной грамотности
обучающихся при обучении математике;
- ни одна из существующих градаций уровней сложности не учитывает
индивидуальные особенности учеников.
С учетом анализа существующих градаций уровней сложности нами были
выделены 4 уровня сложности тестовых задач. В основе выделения этих
уровней лежат следующие основания:
- специфика деятельности при работе с информацией (узнавание,
воспроизведение, применение по заданному алгоритму, применение в
знакомой или не знакомой ситуации или применение в нестандартной
ситуации);
- необходимость применения материла для решения
практико-ориентированных задач;
- учет индивидуальных особенностей обучающихся, в частности, стилевых
особенностей. Бершадский М.Е. считает, что диагностика понимания должна
включать перекодирование информации и установление связей между
понятиями [16]. Такой же точки зрения придерживается Филиппова Д.А.:
умение перекодировать информацию является базовым средством обеспечения
понимания информации [7]. Ею была разработана типология математических
задач на перекодирование, которую мы взяли за основу при разработке
уровней сложности тестовых заданий для диагностики образовательных
результатов по математике.
Рассмотрим предлагаемые уровни сложности:
- Концептуальный (входной)
Ему соответствуют задания, требующие узнавания известной информации,
а также знания теоретического материала, формул, определений. Содержит
задачи, представленные одним способом кодирования.
- Деятельностный (базовый)
Для решения заданий этого уровня сложности требуется воспроизведение
информации и ее применение по образцу (готовому алгоритму). Для этого
уровня характерны задачи, в тексте которых условие и требование содержит
два способа представления информации и требуется перекодирование с
одного способа на другой.
- Комбинированный (продуктивный)
Задания этого уровня сложности требуют применения знаний и умений в
знакомой ситуации, но отличающейся от образца, либо применения знаний и
умений в незнакомой ситуации с известным алгоритмом решения. Для решения
задач этого уровня необходимо уметь применять полученные знания в
реальной жизни. Задания, соответствуют уровню PISA. В тексте задач этого
уровня условие, требование и варианты ответа содержат все три способа
кодирования.
- Углубленный
Задания этого уровня сложности требуют применения знаний и умений в
незнакомой, отличающейся от стандартной ситуации, умения комбинировать
известные способы решения задач, видеть объект с разных сторон,
критически оценивать учебную информацию. Текст задачи также содержит все
три способа кодирования и включает мини-исследование.
Приведем примеры разработанных нами задач для каждого уровня по теме
«Производная функции».
Концептуальный уровень. Образно-графический способ кодирования
информации.
На каком из рисунков продемонстрирован геометрический смысл
производной? Укажите номер.
1)
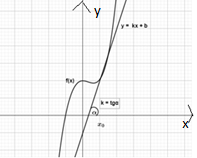 2) 2)
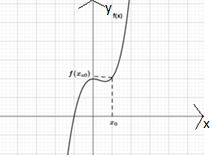 3) 3)
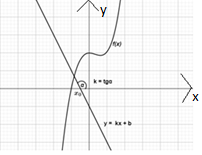
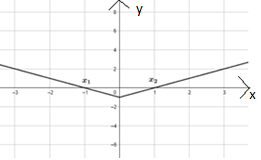
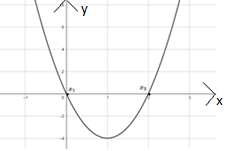
- Деятельностный уровень. Переход с символьного способа кодирования
информации на образно-графический.
Решите уравнение f´(x) = 0, если f(x) = x3 – 3x. Выберите рисунок,
который соответствует графическому представлению решения уравнения.
1) 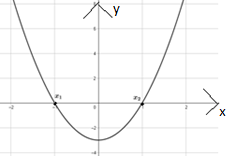 2)
2)  3)
3)
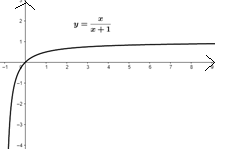
- Комбинированный уровень. Используются все три способа кодирования
информации.
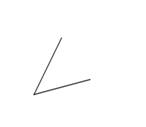
Профиль подъема шоссе имеет форму части кривой, изображенной на
рисунке. На каком рисунке изображена величина угла наклона шоссе в его
начале?
А)
 Б)
Б)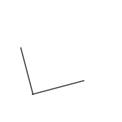 В)
В)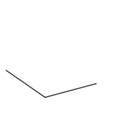
- Углубленный уровень. Необходимо применить знания в незнакомой
ситуации, используя все три способа кодирования информации.
Найдите все значения
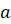 , при
которых значения производной функции , при
которых значения производной функции
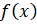 неотрицательны для всех
неотрицательны для всех
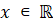 , если , если
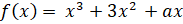 .
Изобразите на числовой прямой найденные значения .
Изобразите на числовой прямой найденные значения
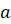 . .
Таким образом, разработанные нами уровни сложности тестовых заданий
(закрытого типа для первых трех уровней и открытого для четвертого), в
которых учитываются различные способы представления математических
задач, могут способствовать индивидуализации процесса обучения, а значит
и повышению уровня успеваемости учеников по математике. Это следует из
исследования [5], в котором говорится о том, что решение задачи в
приоритетном для ученика способе представления или перевод учеником
задачи в приоритетный для него способ представления способствует
улучшению образовательных результатов по математике.
Литература
-
Селевко, Г. К. Современные образовательные технологии: Учебное пособия
[Текст] / Г. К. Селевко. - М.: Народное образование, 1998.
-
Холодная М.А. Когнитивные стили. О природе индивидуального ума. 2-е изд.
– СПб.: – Питер, 2004. – 384 с: ил. – (Серия «Мастера психологии»).
-
Крутецкий В.А. Психология математических способностей школьников. M.:
Институт практической психологии. 1998. 416 с.
-
Якиманская И.С. Развивающее обучение: книга для учителя. М.: Педагогика.
1979. 144 с.
-
Подходова Н.С., Орлова А.В., Снегурова В.И. Стилевые особенности
учащихся как одно из оснований конструирования адаптивных тестов по
математике // Письма в Эмиссия.Оффлайн (The Emissia.Offline Letters):
электронный научный журнал. 2020. №10 (октябрь). ART 2877. URL:
http://emissia.org/offline/2020/2877.htm
. [Дата обращения 01.08.2022]
-
Копелевич Ф.И. Учет индивидуальных особенностей учащихся при обучении
математике: дис. канд. пед. наук: 13.00.02. - СПб., 2004. - 245 с.
-
Филиппова Д.А. Задачи на перекодирование как средство, способствующее
пониманию учебного материала при изучении алгебры в основной школе : дис.
канд. пед. наук: 13.00.02. - СПб., 2012. - 197 с.
-
Милованов Николай Юрьевич Перекодирование как прием формирования у
старшеклассников системы понятий математического анализа // Вестник
Костромского государственного университета. Серия: Педагогика.
Психология. Социокинетика. 2016. №1.
-
Дюндин, А. В. Проблема перекодирования информации в процессе обучения /
А. В. Дюндин // Известия Смоленского государственного университета. –
2008. – № 2. – С. 160-170.
-
Ливер Б.Л. Обучение всего класса. М.: Новая школа, 1995.
-
Хохлова Марина Владиславовна. Методика конструирования системы задач и
ее применение в обучении математике студентов технических вузов : Дис.
... канд. пед. наук : 13.00.02 : Киров, 2004 194 с.
-
Жунусакунова, А. Д. Подходы к определению уровня сложности тестовых
заданий / А. Д. Жунусакунова. — Текст : непосредственный // Молодой
ученый. — 2017. — № 4.1 (138.1). — С. 55-58.
-
Походина Е.Н. Использование тестовых заданий ИИП «КМ – Школа» в
начальной школе. 2009 г. [Электронный ресурс].
URL:
http://www.km-school.ru/r9/uchitel_3.asp
[Дата обращения 01.08.2022]
-
Кузнецов А.А.Информатика. Тестовые задания. / Кузнецов А. А., Пугач В.
И., Добудько Т. В., Матвеева Н. В. - 2-е изд., испр. - М.: БИНОМ.
Лаборатория знаний, 2003. - 232 с.
-
Основные результаты российских учащихся в международном исследовании
читательской, математической и естественнонаучной грамотности PISA‒2018
и их интерпретация / Адамович К. А., Капуза А. В., Захаров А. Б., Фрумин
И. Д.; Национальный исследовательский университет «Высшая школа
экономики», Институт образования. — М.: НИУ ВШЭ, 2019 — 28 с. —200 экз.
— (Факты образования № 2(25)).
-
Бершадский М.Е. Педагогическая диагностика уровня понимания //
Педагогические измерения. 2012. №3.
Рекомендовано к публикации:
Н.С.Подходова, доктор педагогических наук, научный
руководитель работы;
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии
Literature
-
Selevko, G. K. Sovremenny`e obrazovatel`ny`e texnologii: Uchebnoe
posobiya [Tekst] / G. K. Selevko. - M.: Narodnoe obrazovanie, 1998.
-
Xolodnaya M.A. Kognitivny`e stili. O prirode individual`nogo uma. 2-e
izd. – SPb.: – Piter, 2004. – 384 s: il. – (Seriya «Mastera psixologii»).
-
Kruteczkij V.A. Psixologiya matematicheskix sposobnostej shkol`nikov.
M.: Institut prakticheskoj psixologii. 1998. 416 s.
-
Yakimanskaya I.S. Razvivayushhee obuchenie: kniga dlya uchitelya. M.:
Pedagogika. 1979. 144 s.
-
Podxodova N.S., Orlova A.V., Snegurova V.I. Stilevy`e osobennosti
uchashhixsya kak odno iz osnovanij konstruirovaniya adaptivny`x testov
po matematike // Pis`ma v E`missiya.Offlajn (The Emissia.Offline Letters):
e`lektronny`j nauchny`j zhurnal. 2020. №10 (oktyabr`). ART 2877. URL:
http://emissia.org/offline/2020/2877.htm
. [Data obrashcheniya 01.08.2022]
-
Kopelevich F.I. Uchet individual`ny`x osobennostej uchashhixsya pri
obuchenii matematike: dis. kand. ped. nauk: 13.00.02. - SPb., 2004. -
245 s.
-
Filippova D.A. Zadachi na perekodirovanie kak sredstvo,
sposobstvuyushhee ponimaniyu uchebnogo materiala pri izuchenii algebry`
v osnovnoj shkole : dis. kand. ped. nauk: 13.00.02. - SPb., 2012. - 197
s.
-
Milovanov Nikolaj Yur`evich Perekodirovanie kak priem formirovaniya u
starsheklassnikov sistemy` ponyatij matematicheskogo analiza // Vestnik
Kostromskogo gosudarstvennogo universiteta. Seriya: Pedagogika.
Psixologiya. Sociokinetika. 2016. №1.
-
Dyundin, A. V. Problema perekodirovaniya informacii v processe
obucheniya / A. V. Dyundin // Izvestiya Smolenskogo gosudarstvennogo
universiteta. – 2008. – № 2. – S. 160-170.
-
Liver B.L. Obuchenie vsego klassa. M.: Novaya shkola, 1995.
-
Xoxlova Marina Vladislavovna. Metodika konstruirovaniya sistemy`
zadach i ee primenenie v obuchenii matematike studentov texnicheskix
vuzov : Dis. ... kand. ped. nauk : 13.00.02 : Kirov, 2004 194 s.
-
Zhunusakunova, A. D. Podxody` k opredeleniyu urovnya slozhnosti
testovy`x zadanij / A. D. Zhunusakunova. — Tekst : neposredstvenny`j //
Molodoj ucheny`j. — 2017. — № 4.1 (138.1). — S. 55-58.
-
Poxodina E.N. Ispol`zovanie testovy`x zadanij IIP «KM – Shkola» v
nachal`noj shkole. 2009 g. [E`lektronny`j resurs]. URL:
http://www.km-school.ru/r9/uchitel_3.asp
[Data obrashcheniya 01.08.2022]
-
Kuzneczov A.A.Informatika. Testovy`e zadaniya. / Kuzneczov A. A.,
Pugach V. I., Dobud`ko T. V., Matveeva N. V. - 2-e izd., ispr. - M.:
BINOM. Laboratoriya znanij, 2003. - 232 s.
-
Osnovny`e rezul`taty` rossijskix uchashhixsya v mezhdunarodnom
issledovanii chitatel`skoj, matematicheskoj i estestvennonauchnoj
gramotnosti PISA‒2018 i ix interpretaciya / Adamovich K. A., Kapuza A.
V., Zaxarov A. B., Frumin I. D.; Nacional`ny`j issledovatel`skij
universitet «Vy`sshaya shkola e`konomiki», Institut obrazovaniya. — M.:
NIU VShE`, 2019 — 28 s. —200 e`kz. — (Fakty` obrazovaniya № 2(25)).
-
Bershadskij M.E. Pedagogicheskaya diagnostika urovnya ponimaniya //
Pedagogicheskie izmereniya. 2012. №3.
|
 2)
2)
 3)
3)

 2)
2)  3)
3)



