Abstract
The article deals with the description of the implementation of the adaptive testing system in learning process. This system was built on three bases: levels of complexity of tasks, typology of mathematical problems, information coding styles. Examples of tasks of different blocks of the system are given. 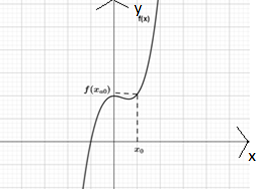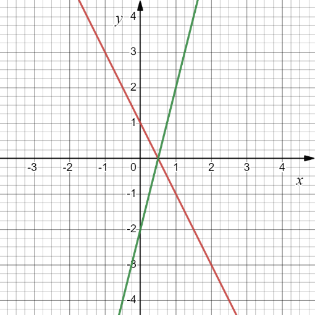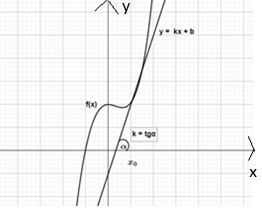The results of testing this system showed that the use of adaptive testing system helps to increase the level of assimilation of the material of students and comprehension.

Key words: adaptive test, information coding styles, diagnostics of knowledge and skills of students.

----------------

В настоящее время актуальна проблема индивидуализации обучения, неотъемлемой частью которой является проблема эффективной организации контроля уровня знаний обучающихся. В свою очередь, развитие дистанционных технологий требует обновления способов и средств объективного оценивания учебных достижений учащихся. Всё это стало причиной появления адаптивных систем тестирования, основанных на принципе индивидуализации обучения. Существует достаточно много трактовок понятия адаптивного теста, так же как и подходов к организации системы адаптивного теста. Традиционно под адаптивным тестом понимается электронная система проверки и оценки результатов обучения, с возможностью оптимизации подбора количества заданий, их сложности и других заданных характеристик [1], [2]. Из определения видно, что основным преимуществом адаптивного теста является возможность учета индивидуальных характеристик обучающихся. Анализ литературы, посвященной проблеме учета индивидуальных особенностей учащихся в процессе обучения, показал, что стилевые особенности, в частности, когнитивные стили, оказывают влияние на успешное овладение и понимание материала [3], [4].

Ранее нами были проанализированы различные подходы к построению системы адаптивного тестирования [5]. Было показано, что ни один из существующих подходов не учитывает индивидуальные особенности обучающихся. Поэтому нами разработан новый подход, который предполагает блочную структуру адаптивного теста и учитывает три основания: типологию математических задач, уровни сложности задач, стили кодирования информации [5]. Для того, чтобы проверить эффективность предложенного подхода к системе адаптивного тестирования, нами была проведена апробация разработанных материалов. Апробация проводилась при изучении тем «Производная и ее геометрический смысл» и «Приложения производной».

В исследовании приняли участие 115 студентов 1 курса среднего профессионального образования (16-17 лет, 64 девушки и 51 юноша). Из них 56 обучающихся входили в экспериментальную группу, 59 обучающихся – в контрольную группу. Экспериментальная группа работала в компьютерных классах. Изначально каждый студент экспериментальной группы проходит входное тестирование. В результате этого тестирования определяется приоритетная для каждого обучающегося форма представления информации (образно-графическая, вербальная или символьная). На основании полученных данных каждый студент проходит индивидуальный маршрут, включающий три этапа адаптивного тестирования в течение изучения темы.

Первый этап реализуется через тестовые задания концептуального блока. Они предлагались обучающимся сразу после введения базовых понятий, т.к. этот блок направлен на диагностику усвоения теоретических компонентов темы. Задания система предлагает разным студентам разные, в зависимости от его приоритетной формы представления информации, выделенной и зафиксированной в системе на этапе входного тестирования, то есть в образной, вербальной и символьной стратегии. Приведем пример задач из этого блока по указанным темам.

Тема «Производная и ее геометрический смысл»

Концептуальный блок (образная стратегия)

На каком рисунке отражен геометрический смысл производной функции f(x) в точке ?

1) 2) 

3)

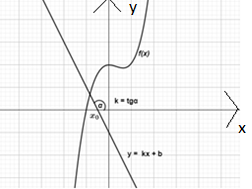
Рис.1. Геометрический смысл производной

Тема «Приложения производной»

Концептуальный блок (вербальная стратегия)

Пусть – точка экстремума функции f(x). Выберите верные утверждения:

1. Значение производной функции в точке равно нулю.
    
2. Значение производной функции в точке либо положительно, либо отрицательно.
    
3. Касательная, проведенная к графику функции f(x) в точке с абсциссой параллельна оси абсцисс.
    
4. Значение функции в точке равно нулю.
    
5. При переходе через точку производная функции меняет свой знак.

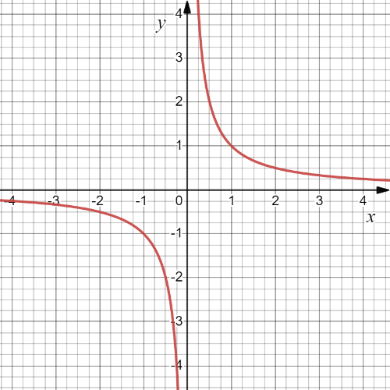
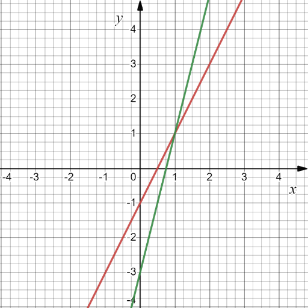
Количество заданий в концептуальном блоке зависит от количества теоретических единиц, заданных для усвоения в данной теме. После прохождения тестов концептуального блока по каждой теме каждому обучающемуся предъявлялся его результат. В случае, если в каком-либо задании блока была допущена ошибка, студенту предлагалось изучить соответствующий теоретический материал Например, если ошибка была допущена в задании, направленном на усвоение геометрического смысла производной, обучающемуся может быть предложено посмотреть видео-урок, размещенный на платформе «Российская электронная школа», по теме «Геометрический смысл производной» (https://resh.edu.ru/subject/lesson/3976/main/201108/)

Второй процессуальный блок предполагал диагностику умений, которыми должен овладеть учащийся в рамках изучения определенной темы. К выполнению заданий концептуального блока обучающиеся приступали после этапа первичного закрепления, т.к. этот блок направлен на диагностику усвоения умений по изучаемой теме. Задания в этом блоке предполагали переход от приоритетной формы представления информации в неприоритетную с целью развития стилевой гибкости ученика. Приведем пример задачи из этого блока.

Тема «Производная и ее геометрический смысл»

Процессуальный блок (из вербальной стратегии в образную)

Постройте касательную к графику функции, который изображен на рисунке, в точке = 1. Выберите верные утверждения об угловом коэффициенте и свободном члене уравнения этой касательной:

Рис. 2. График функции

1. Угловой коэффициент положительный, свободный член отрицательный.
    
2. Угловой коэффициент отрицательный, свободный член положительный.
    
3. Угловой коэффициент и свободный член положительный.
    
4. Угловой коэффициент и свободный член отрицательный.

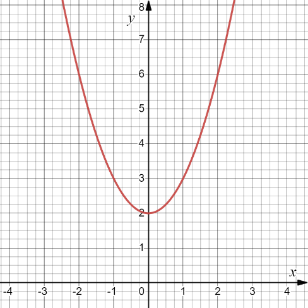
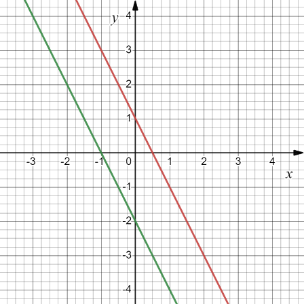
В случае, если ошибка была допущена при диагностики умения применять производную к построению графиков функций, студенту предлагается разобрать решение соответствующей задачи из ГДЗ (например, решение задачи № 917 [6]).

Задания третьего уровня сложности предлагаются в рамках комбинированного блока, реализуемого преимущественно на этапах повторения, обобщения и систематизации. Этот блок содержит задания, в которых присутствуют все три формы представления информации. Приведем примеры заданий этого блока.

Тема «Производная и ее геометрический смысл»

Комбинированный блок

Заданы две функции f(x) и g(x), где  , а график функции g(x) изображен на рисунке.

Рис. 4. График функции g(x)

На какой картинке изображены общие касательные к графикам функций f(x) и g(x)?

 А)    Б)

В)

Рис. 5. Общие касательные к графикам функций

Тема «Приложения производной»

Комбинированный блок

Дана функция y = f(x). Известно, что f’(x) < 0 на , f’(x) > 0 на  , значение производной функции в точке -2 и значение производной функции в точке 0 равно 0, значение функции в точке -2 равно -1, а f(0) = 3. Постройте эскиз графика функции. Найдите промежутки монотонности функции и точки экстремума.

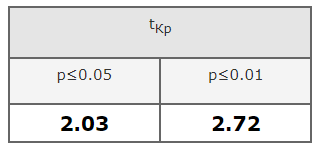
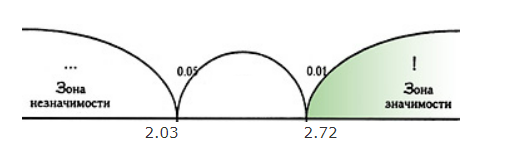
Студенты контрольной группы по каждой теме решали контрольную работу по этим же темам согласно программе. После каждой контрольной работы с обучающимися был выполнен анализ результатов, проработаны типичные ошибки. После изучения двух тем студентам обеих групп была предложена одна и та же итоговая контрольная работа по изученным темам согласно программе.

Было проведено сравнение результатов итоговой контрольной работы, выполненной обучающимися экспериментальной и контрольных групп. Для расчета достоверности различий между результатами контрольной работы был использован t-критерий Стьюдента. Было получено значение t = 3.9. Критические значения t-критерия представлены в таблице 1.

Таблица 1

Критические значения t-критерия

Таким образом, полученное значение t = 3.9 находится в зоне статистической значимости (рис.5).

Рис. 6. Зона значимости t-критерия

Анализ полученных результатов подтверждает, что применение адаптивного тестирования на этапе контроля знаний позволяет контролировать процесс развития каждого ученика, диагностировать пробелы в отдельных компонентах темы и своевременно их устранять. Отсюда можно сделать вывод, что разработанная система адаптивного тестирования является эффективным инструментом реализации индивидуализации обучения. А учет таких когнитивных особенностей обучающихся как стили кодирования информации, позволяют им изучить математический объект с разных сторон, что способствует пониманию и более успешному овладению материала по сравнению с традиционным методами.

Литература

1. Строгонова, Е. И. Технологии компьютерного адаптивного тестирования системы контроля и оценки знаний, обучающихся в условиях компетентностного подхода // Восточно-Европейский научный журнал. 2016. Т. 10. № 1. С. 118-122.

2. Здорова Л. А. Разработка системы адаптивных компьютерных тестов: учебное пособие. Владивосток: Морск. гос. ун-т им. адм. Г.И. Невельского, 2006. 90 с.

3. Н.С.Подходова, А.В.Орлова, В.И.Снегурова. Стилевые особенности учащихся как одно из оснований конструирования адаптивных тестов по математике // Письма в Эмиссия.Оффлайн (The Emissia.Offline Letters): электронный научный журнал. 2020. №10 (октябрь). ART 2877. URL: http://emissia.org/offline/2020/2877.htm [Дата обращения 02.05.2023]

4. Jantan, R.B. Relationship between Students’ Cognitive Style (Field Dependent and Field-Independent Cognitive Styles) with their Mathematic Achievement in Primary School. International Journal of Humanities Social Sciences and Education. 2014. vol. 1. no. 10. P. 88-93.

5. Беленко А.Г., Подходова Н.С. Принципы разработки системы адаптивного тестирования по математике на основе учета когнитивных особенностей обучающихся // Современные проблемы науки и образования. 2023. № 2. URL: https://science-education.ru/ru/article/view?id=32570 [Дата обращения 02.05.2023]

6. Кадеев А.А. Домашняя работа по алгебре и началам математического анализа за 11 класс к учебнику Ш.А. Алимова и др. «Алгебра и начала математического анализа . 10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень» / А.А. Кадеев, О.Г. Перфильева. – 11-е изд., перераб. и испр. – М.: Издательство «Экзамен», 2014. – 319 с.

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

Literature

1. Strogonova, E. I. Tekhnologii komp'yuternogo adaptivnogo testirovaniya sistemy kontrolya i ocenki znanij, obuchayushchihsya v usloviyah kompetentnostnogo podhoda // Vostochno-Evropejskij nauchnyj zhurnal. 2016. T. 10. № 1. S. 118-122.

2. Zdorova L. A. Razrabotka sistemy adaptivnyh komp'yuternyh testov: uchebnoe posobie. Vladivostok: Morsk. gos. un-t im. adm. G.I. Nevel'skogo, 2006. 90 s.

3. N.S.Podhodova, A.V.Orlova, V.I.Snegurova. Stilevye osobennosti uchashchihsya kak odno iz osnovanij konstruirovaniya adaptivnyh testov po matematike // Pis'ma v Emissiya.Offlajn (The Emissia.Offline Letters): elektronnyj nauchnyj zhurnal. 2020. №10 (oktyabr'). ART 2877. URL: http://emissia.org/offline/2020/2877.htm [Data obrashcheniya 02.05.2023]

4. Jantan, R.B. Relationship between Students’ Cognitive Style (Field Dependent and Field-Independent Cognitive Styles) with their Mathematic Achievement in Primary School. International Journal of Humanities Social Sciences and Education. 2014. vol. 1. no. 10. P. 88-93.

5. Belenko A.G., Podhodova N.S. Principy razrabotki sistemy adaptivnogo testirovaniya po matematike na osnove ucheta kognitivnyh osobennostej obuchayushchihsya // Sovremennye problemy nauki i obrazovaniya. 2023. № 2. URL: https://science-education.ru/ru/article/view?id=32570 [Data obrashcheniya 02.05.2023]

6. Kadeev A.A. Domashnyaya rabota po algebre i nachalam matematicheskogo analiza za 11 klass k uchebniku SH.A. Alimova i dr. «Algebra i nachala matematicheskogo analiza . 10-11 klassy: ucheb. dlya obshcheobrazovat. uchrezhdenij: bazovyj uroven'» / A.A. Kadeev, O.G. Perfil'eva. – 11-e izd., pererab. i ispr. – M.: Izdatel'stvo «Ekzamen», 2014. – 319 s.